Решение уравнения Шрёдингера для частицы, находящейся в одномерной бесконечно глубокой потенциальной яме. Анализ решения

15. Решение уравнения Шрёдингера для частицы, находящейся в одномерной бесконечно глубокой потенциальной яме. Анализ решения.

Потенциальная яма – ограниченная область пространства, в которой потенциальная энергия частицы меньше, чем за ее пределами.

Рассмотрим состояния частицы, находящейся в одномерной прямоугольной бесконечно глубокой потенциальной яме. Потенциальная энергия частицы в зависимости от координаты x изображена на рисунке 1.

 При 0<x<a потенциальную энергию частицы можно принять равной нулю, а вне этого интервала она обращается в бесконечность. Вследствие этого частица при своем движении не может выйти за пределы (0, а). Поскольку вероятность нахождения частицы вне интервала (0, a) равна нулю, то и Ψ - функция вне этого интервала равна нулю. А так как она должна быть непрерывной функцией во всей области координат, то в точках x=0 и x=a она обращается в нуль. Таким образом, для функции Ψ(x) получаются следующие граничные условия:                         Ψ(0)=Ψ(а)=0

Уравнение Шредингера внутри ямы, где потенциальная энергия равна нулю, имеет вид         (3)

где принято обозначение                                                                          (4)

Общее решение этого уравнения таково    Граничное условие Ψ(0)=0 дает B=0, а из граничного условия Ψ(а)=0 следует, что,   

 аχ=nπ,                        (5)          где n=1,2,3,…                                               

На основании соотношений (4) и (5) получаем выражение для уровней энергии 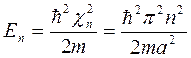   . (6) 

   Это условие квантует энергию частицы. Формула (6) показывает, что существует некоторая минимальная энергия, не равная нулю, соответствующая состоянию движения частиц.         

Волновая функция этого состояния    ни в какой точке интервала (0, а) не обращается в нуль. Свойство волновой функции имеет общий характер: волновая функция основного состояния не имеет узлов, т.е. не обращается в нуль внутри рассматриваемой области, а может обращаться в нуль только на границах.

Из формулы (6) видно, что при увеличении линейного размера ямы минимальная энергия уменьшается. Физическая причина состоит в том, что при уменьшении размеров ямы уменьшается длина волны де Бройля, а уменьшение длины волны означает увеличение энергии частицы. Поскольку спектр дискретен, условие нормировки

  

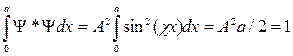
 для нормировочного множителя дает                  

  Поэтому система собственных функций имеет вид: 

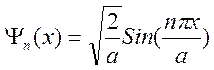.                                                   (7)

Анализ решения:

1.  записать и найти решение стац-го ур-ия Шрёдингера для каждой области пространства, где U=const, отдельно

2.  потребовать выполнение стандартных условий для ψ(x)                  

                                            а)  конечность ψ(x) во всей области x

                                            б) потребовать выполнение условия непрерывности функции ψ(x)

                                             ψ_I(0)= ψ_II(0)           ψ_II(а)= ψ_III(а)   -                      

                                            в)  выполнить требования непрерывности

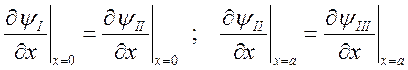
3.  из условий 2б и 2в получить формулу для энергии частицы Е

4.    пользуясь условием нормировки функции ψ(х), определить значение постоянной величины в этой ф-ции.