






Лекция 10.
VI. Распространение света в анизотропных средах (Кристаллооптика).
Описание анизотропных сред.
Рассматривая закономерности распространения света в различных средах, мы предполагали, что они оптически изотропны, т.е. скорость света в каждой точке среды не зависит ни от направления распространения световой волны, ни от характера поляризации волны.
При обычных условиях газообразные, жидкие и твердые аморфные диэлектрики оптически изотропны. В то же время, почти все кристаллические диэлектрики анизотропны. Также под влиянием внешних воздействий среда, бывшая оптически изотропной, может стать оптически анизотропной. Прохождение света в таких средах сопровождается дополнительными эффектами.
Закономерности распространения света в любой среде (изотропной или анизотропной) в конечном счете определяются интерференцией первичной волны и вторичных волн, излучаемых молекулами, атомами или ионами среды вследствие их электронной поляризации под действием электрического поля Е световой волны. Поэтому оптические свойства среды полностью обусловлены электрическими свойствами этих элементарных излучателей, их взаимным расположением и взаимодействием друг с другом.
Молекулы и атомы среды в зависимости от их строения могут быть электрически изотропными или анизотропными. В первом случае их поляризуемость не зависит от направления, во втором – зависит. Однако электрические свойства отдельных атомов или молекул среды еще не определяют полностью оптические свойства этой среды. Так газы, жидкости, аморфные твердые тела изотропны, хотя молекулы многих из них электрически анизотропны. Причина этого – полная хаотичность ориентаций молекул. Упорядочение же ориентаций анизотропных молекул в этих средах под влиянием внешних воздействий приводит к возникновению оптической анизотропии.
Если среда находится в кристаллическом состоянии, то ее частицы (атомы, молекулы или ионы) располагаются в строгом порядке, образуя кристаллическую решетку. Каждая частица находится в сильном взаимодействии с ближайшими соседями в решетке. Поэтому излучение вторичных волн частицами кристаллической среды зависит не только от электрических свойств самих частиц, но и от силового воздействия со стороны других частиц. Т. обр. оптическая анизотропия кристалла может быть обусловлена как электрической анизотропией образующих его частиц, так и анизотропией поля сил взаимодействия между частицами. Характер этого поля, т. е. его изотропность, или анизотропность зависит от степени симметрии решетки кристалла. Только кристаллы кубической системы (например, каменная соль NaCl) обладают весьма высокой степенью симметрии решетки и являются оптически изотропными. Все остальные кристаллы независимо от электрических свойств образующих их частиц оптически анизотропны.
Расчет интерференции вторичных волн в анизотропных кристаллах весьма сложен. Более простой метод изучения закономерностей распространения света в таких средах основывается на применении к ним теории Максвелла для переменного электромагнитного поля. При этом кристалл рассматривается как однородная среда, электрическая поляризуемость æ и относительная диэлектрическая проницаемость ε=1+æ которой неодинаковы в различных направлениях. Предполагается, что кристалл немагнитен, т. е. μ=1.
Таким образом считается, что оптическая анизотропия обычных кристаллов является следствием анизотропии его относительной диэлектрической проницаемости.
Если однородная среда непоглощающая и оптически неактивна, то зависимость ε от направления поддается сравнительно простой графической интерпретации.
Из произвольной точки О среды по различным направлениям будем проводить
радиус-векторы ![]() , причем
, причем ![]() в
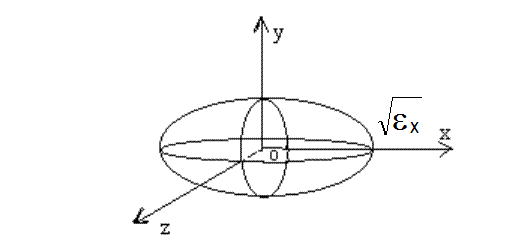
данном направлении. Поверхность, проходящая через концы радиус-векторов имеет
форму эллипсоида и называется оптической индикатрисой
в
данном направлении. Поверхность, проходящая через концы радиус-векторов имеет
форму эллипсоида и называется оптической индикатрисой
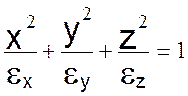 |
 ,
где
εx, εy, εz,-
главные значения диэлектрической проницаемости среды.
,
где
εx, εy, εz,-
главные значения диэлектрической проницаемости среды.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.