Понятие функции. Предел функции в точке

§ 16. Понятие функции. Предел функции в точке.

16.1. Определение функции.

(самостоятельно)

16.2. Способы задания функции.

(самостоятельно)

16.3. Классификация функций.

Простейшие элементарные функции – это постоянная функция (если $ c Î R такая, что " x Î D(f) f(x) = с = const), степенная (a Î R фиксированное число; x^a), показательная (y = a^x_, 0 < a ¹ 1), логарифмическая (log_ax, 0 < a ¹ 1), тригонометрическая (sin, cos, tg, ctg), обратно тригонометрическая (arcsin, arccos, arctg, arcctg).

Все функции, полученные из простейших конечным числом арифметических операций и суперпозиций образуют класс элементарных функций.

q  f(x) = |x| = ;

f(x) = lg³arctg+ sin3x...

Классификация элементарных функций.

1) P(x) = a₀x^m+…+a_m, m ³ 0 – целое число, a₀ ¹ 0, a₁, …, a_m – произведение фиксированного числа. P(x) называется целой рациональной функцией или многочленом.

2) P(x) = 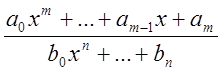 – дробно-рациональная функция.

1) и 2) – рациональные функции.

3) функции, полученные с помощью конечного числа суперпозиций и четырех арифметических действий над смешенными функциями с любым показателем и не являющиеся рациональными называются рациональными функциями. f(x) = .

4) каждая функция, не являющаяся рациональной или иррациональной называется трансцендентной. f(x) = sinx + x.

16.4. Предел функции в точке.

Сначала определим предел функции в точке «по Гейне», то есть на языке последовательностей.

Пусть функция f(x) определена на некотором множестве X Ì R и пусть x₀ – предельная точка множества X (x₀ Î X или x₀ Ï X). Возьмем последовательность (x_n) точек из X, сходящейся к x₀. Значения функции f в этих точках образуют последовательность.

f(x₁), f(x₂), …, f(x_n), …

и можно ставить вопрос о существовании ее предела.

Определение 1. Число A называют пределом функции f(x) в точке x = x₀ (или при x ® x₀), если для каждой сходящейся к x₀ последовательности (x_n) точек из D(f) (отличных от x₀) соответствующая последовательность (f(x_n)) сходящейся к числу A.

Обозначение lim f(x) = A.

                         ^{x ® x}0

Функция имеет только один предел.

q  1) f(x) = C = const

lim f(x) = C.

  ^{x ® x}0

2) f(x) = x (f(x_n) = x_n) lim f(x) = x₀.

                                      ^{x ® x}0

3) f(x) = sin () (x ¹ 0)

не имеет предела при x ® 0.

а) x_n =    ®   0  f(x_n) = sin np = 0 ® 0

                       ^{n ® ¥}

 б) x_n = 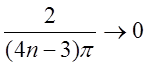 f(x_n) = sin (2np – p) = 1 ® 1

0¹ 1, то есть предел последовательности значений функции зависит от выбора последовательностей значений аргумента, сходящейся к точке x = 0. Следовательно, f(x) не имеет предела в этой и точке.

4) f(x) = 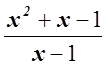имеет в точке x = 0 предел, равный 1.

 " (x_n): x_n ® 0 и x_n ¹ 0

lim f(x_n) = lim 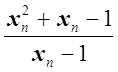= = 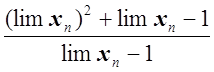 = 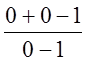1

 ^{n ® ¥               n ® ¥}

Существует и другое определение предела функции.

Определение 2. Число A называется пределом функции f(x) в точке x = x₀, если " e > 0 $ d > 0  "x Î x ((x ¹ x₀, |x – x₀| < d) Þ |f(x) – A| < e). Это определение «на языке e – d» принадлежит Огюстену Коши (21.08.1789 – 1857) французскому математику. Генрих Гейне – немецкий математик (1821 – 1881)

Теорема 16.1 Первое и второе определения предела функции совпадают.

 1) Пусть A – предел f(x) в точке x₀ согласно первому определению. Покажем, что A – предел согласно второму определению. Предположим обратное, то есть A не является пределом этой функции согласно второго определения. Это означает, что не для всякого e > 0 можно указать такое d > 0, чтобы из неравенства 0 < |x – x₀| < d следовало неравенство |f(x) – A| < e. Следовательно, существует такое e = e₀ > 0, что " d > 0 найдется хотя бы одна точка x ¹ x₀ для которой |x – x₀| < d, по |f(x) – A| ³ e₀.

Найдя такое e₀, будем выбирать в качестве d последовательно числа: 1;  , …, … Тогда для d_n =  выберем такое x_n, чтобы 0 < |x_n – x₀| <  и |f(x_n) – A| ³ e₀.

В результате получаем последовательность (x_n) точек, отличающихся от x₀ и сходящихся к x₀. (Проверьте последнее)

В соответствии с определением 1 последовательность (f(x_n)) должна сходиться к A. Это, в частности, означает, что для выбранного e₀ > 0 найдется n₀ такое, что " n ³ n₀ |f(x_n) – A| < e₀. Но это противоречит тому факту, что "n Î N |f(x_n) – A| ³ e₀.

Полученное противоречие показывает, что A должно быть пределом f(x) в точке x₀ и по определению 2.

2) Пусть теперь A – предел функции f(x) согласно определению 2, то есть " e > 0 $ d > 0: " x Î x (0 < |x – x₀| < d Þ |f(x) – A| < e). Тогда рассмотри произведение последовательности (x_n) точек, отличных от x₀ и сходящихся к x₀.

Докажем, что (f(x_n)) сходится к A. Для этого фиксируем произведение e > 0 и по нему с помощью определения 2 найдем соответствующее d > 0.

Далее, по числу d > 0 найдем n₀ Î N такое, что " n > n₀ 0 < |x_n – x₀| < d. Для этих же n в силу выбора d имеем |f(x_n) – A| < e. Но это означает, что " e > 0 найдется n₀ такое, что " n ³ n₀ |f(x_n) – A| < e. Следовательно, lim f(x_n) = A.

В силу произвольности последовательности (x_n) получаем, что A – предел f(x) и по определению 1.

16.5. Односторонние пределы (при x® x₀+ и при x® x₀-).

Определение 3. ЧислоA называется правым (левым) пределом функции f(x) в точке x₀, если для любой сходящейся к x₀ последовательности (x_n), элементы которой больше (меньше) x₀, соответствующая последовательность (f(x_n)) сходящейся к A.

lim f(x) = A (lim f(x) = A).

^{x ® x}0^{+                 x ® x}0^-

                                +1, x > 0;

q  f(x) =  sign x =       0, x = 0;

     –1, x < 0.

lim f(x) = sign x

^{x ® 0+}

Задание: сформулируйте определение односторонних пределов функции f(x) «на языке e – d».

Теорема 16.2. f(x) имеет в точке x₀ предел тогда и только тогда, когда в этой точке $ как правый, так и левый пределы и они равны. В этом случае предел функции равен односторонним пределом.

 Доказательство придумать самостоятельно или выучить его с помощью книги В.С. Шипачева «Высшая математика» стр. 77.

16.6. Предел функции при x®¥, при x® –¥, при  x® +¥.

Определение 4. Число A называется пределом функции f(x) при x ® ¥, если для любой бесконечно большой последовательности (x_n) последовательность (f(x)) сходится к A.

Определение 5. A = lim f(x), если " бесконечно большой последовательности (x_n) с положительным (отрицательным) членами последовательности (f(x_n)) сходящихся к A. и т.д.

q  f(x) =  ,   lim  = 0

    ^{x ® ¥}

16.7. Теоремы о пределах функций.

Определение предела функции на языке последовательностей позволяет перенести рассмотренные ранее теоремы о пределах последовательностей на функции.

Теорема 16.3. Пусть f(x) и g(x) имеют в точке x₀ пределы В и С. Тогда f(x) ± g(x), f(x)×g(x) и f(x)/g(x) (при C ¹ 0) имеют пределы в точке x₀, равные соответственно B ± C, B×C, и .

…

Теорема 16.4. Пусть f(x), g(x), h(x) определены в некоторых окрестностях точки x_0, за исключением, быть может, самой точки x₀, и функции f(x), h(x) имеют в точке x₀ предел, равный A. Пусть, кроме того, f(x) £ g(x) £ h(x) " x Î x. Тогда lim g(x) = A.

                                                      ^{x ® x}0

Замечание: Теоремы 16.3 и 16.4 справедливы и в случае, когдаx₀ является одним из символов +¥, –¥, ¥.