§ 9. Простейшая форма предельного перехода – предел последовательности
Предел последовательности – простейшая форма предельного перехода. К нему сводятся и другие формы предельного перехода – предел функции, производная, интеграл.
9.1 Повторение способа задания и геометрическое изображение последовательности. Последовательность действительных чисел называется отображение NÎR x: N→R. D(x) =N, E(x)Ì R. xn=x(n); (x1, x2,…xn,…); (xn).
Способы задания последовательности:
1) Аналитический (формула n-ого члена);
2) Рекуррентный (возвратный).
an+1=an+d; bn+1=bn∙q.
Последовательность Фибоначчи:
x1=x2=1; "n³2; xn+1=xn+xn-1; (1;1;2;3,5,…)
Числовой прямой называется множество R действительных чисел введенной структурой полного архимедовски упорядоченного поля.
Способы геометрического изображения последовательности:
а) точками числовой прямой R;
б) точками числовой плоскости R2.
(1/n)
а) x4 x3 x2 x1
0 ¼ ⅓ ½ 1
б)
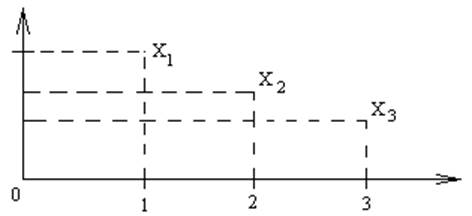
Две последовательности (xn) и (yn) равны тогда и только тогда когда "nÎN xn=yn , но при этом две различные последовательности могут изображаться одним и тем же множеством точек
(1; 2; 3; 4; …) ↔ xn = n
(2; 1; 4; 3; …) ↔ yn = {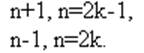
9.2. Операции над последовательностями
def
1) (xn) ± (yn)=(xn±yn)
2)(xn) ∙ (yn)=(xn · yn)
Соглашение. Вместо выражение “все, за исключением конечного числа” будем говорить “почти все”.
Опр. Пусть (xn) и (yn) – две последовательности, причем почти все yn отличны от нуля. Частным (xn) и (yn) назовем (zn), где
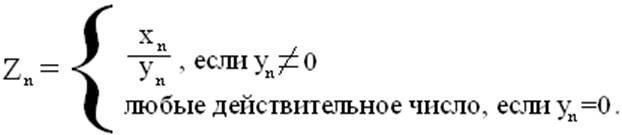
9.3 Ограниченные и неограниченные последовательности.
Опр. Последовательность (xn) д.ч. называется ограниченной (обознач. xn=0(1)), если существует число М ³ 0, такое, что "nÎN|xn| ≤ M. xn=0(1) Û $ M ³ 0: "nÎN |xn| ≤M
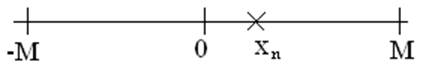
Примеры:
1) "nÎN xn=1;
2) "nÎN xn=1/n;
3) "nÎN xn=(-1)n.
xn ≠ 0(1) Û "M ³ 0 $nÎN (|xn| ³ M
Примеры:
4) "nÎN xn=n;
5) "nÎN xn=-n;
6) "nÎN xn=(-1)nn.
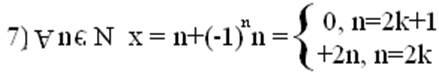
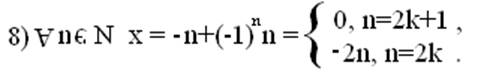
Т. О., множество всех последовательностей можно разбить по на ограниченные и неограниченные.
9.4 Классификация последовательностей по сходимости.
О.1: Будем говорить, что последовательность (Xn) д.ч. сходящихся к действительному числу x0, если для любого ε>0 можно указать pÎN такое, что для всех n≥p вып-ся неравенство /
|xn-x0| ≤ ε, и писать: lim xn = x0 или xn→x0, а саму последовательность (xn) называть сходящейся к x0.
Геометрически сходимость в R означает: в произвольную, сколь угодно малую ε-окрестность т. x0 попадают почти все члены (xn)
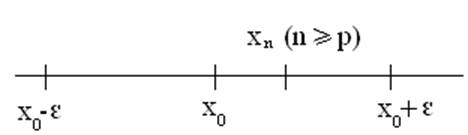
O.1: lim xn=x0 Û ("ε>0 $pÎN ("nÎN; n³ p) Þ |xn-x0| ≤ ε).
Пр. (1) lim xn=1
Пр. (2) lim xn=0
Теорема 1. Если последовательность xn сходится в R, то ее предел единственный.
(частный случай доказан выше, в n)
Пусть lim xn=x0 и lim xn=x’0 на основании определения 1
"ε>0 $p1ÎN ("nÎN; n³p1) Þ |xn-x0|≤ ε/2,
$p2ÎN ("nÎN; n³p2) Þ |xn-x′0|≤ ε/2.
Тогда "n³p=max{p1;p2}
|x0-x′0| = |x0-xn+xn-x′0|≤|x0-xn|+|xn-x′0|≤ ε/2+ ε/2= ε.
Т.к. "ε>0 0≤|x0-x′0|≤ ε, то |x0-x′0|=0 Þ x0=x′0
Теорема 2: Если последовательность (xn) сходящихся в R, то она ограничена.
lim xn=x0ÎR. Из определения предела для ε=1 найдется pÎN ("n³p Þ |xn-x0|≤ 1)
Иначе говоря, "n³p x0-1≤xn≤ x0+1
Рассмотрим M=max {|x1|; |x2|;…; |xn-1|; |-1+x0|; |1+x0|}. Тогда "nÎN|xn| ≤ M
Замечание.Обратное утверждение неверно: |xn|=(-1)n
Опр.2: Будем говорить, что последовательность (xn) действительных чисел сходящихся к +
, если "εÎR
можно указать pÎN такая, что для
всех номеров n³p верно неравенство: xn³ ε; и писать lim xn =
+.
lim xn =
+ Û ("εÎR $pÎN
("nÎN;n³p) Þ xn³ ε).
Геометрически
сходимость к + означает,
что на любой луч (-
,ε]
попадают почти все члены последовательности.
Опр.3: lim xn = - Û ("εÎR $pÎN
("nÎN;n³p) Þ xn≤ ε).
На любой луч вида (-,ε]
попадают почти все члены последовательности.
Сходимость в R.
|
Сходятся в R |
Сходятся к + |
Сходятся к - |
Теорема 1: Если последовательность сходится в R, то ее предел единственный.
Если последовательность не сходится в R, то ее называютколеблющейся.
(3), (6), (8) – колеблющиеся.
Если ограниченная последовательность колеблется, то ее называют неограниченно колеблющейся.
(3) – ограниченно колеблется.
(6)-(8) – неограниченно колеблется.
Множество последовательно разбивается на 5 классов.
|
I Сходится в R |
II Ограниченно колеблется |
III Неограниченно колеблется |
IV Сходится к + |
V Сходятся к - |
Прим. I-II – ограниченные, III-V – неограниченные.
Последовательность (xn)
называется колеблющейся, если она не сходится ни к конечному пределу, ни к +
, ни к -.
9.6 Заключение.
1. Изменение любого конечного количества членов последовательности не влияет на ее сходимость.
2. Изменение бесконечного числа последовательности может как сказаться, так и не сказаться на ее сходимости.
3. Предел x0ÎR может быть одним из значений принимаемых последовательностью.
4. Предел не обязан быть одним из значений, принимаемых последовательностью.
5. Высказывание:
А) "ε>0 "εÎN ("nÎN, n≥p) Þ |xn-x0|≤ε равносильно высказываниям:
B) "ε>0 $pÎN("nÎN, n≥p) Þ |xn-x0|<ε ;
C) "ε>0 неравенство |xn-x0|≤ε выполняется для почти всех номеров nÎN;
D) "ε>0 неравенство |xn-x0|>ε выполняется не более, чем для конечного числа номеров nÎN.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
