Понятие непрерывности функции. Непрерывность некоторых элементарных функций

§ 19. Понятие непрерывности функции.

19.1. Определение непрерывности функции.

Пусть функция f(x) определена в некоторой окрестности точки x₀.

Определение 1. Функция f(x) называется непрерывной в точке x₀, если предел функции и ее значение в этой точке равны, то есть

lim f(x) = f(x)             (*)

Так как lim x = x₀, то равенство (*) можно записать так: lim f(x) = f(lim x).

Таким образом, для непрерывной функции f и lim можно менять местами;

На языке последовательностей:

f непрерывна в точке x₀ Û "(x_n) ((x_n ® x₀) Þ (f(x_n) ® f(x₀)).

На «языке e - d»:

f непрерывна в точке x₀ Û "e > 0 $ d > 0: "x Î x (|x – x₀| < d Þ |f(x) – f(x₀)| < e).

Аналогично определяется непрерывность функции слева и справа. Очевидно, что если функция f(x) непрерывна в точке x₀ и слева и справа, то она непрерывна в этой точке.

Определим понятие непрерывности функции в точке через приращения аргумента и приращения функции.

Dx = x – x – приращение аргумента x в точке x₀, а Dy = f(x₀ + Dx) – f(x₀) – приращение функции f в точке x₀, отвечающее приращению Dx. (Dy = Dy(x₀, D x))

Легко видеть, что lim f(x) = f(x₀) Û lim Dy = 0.

Отсюда и определение 2: Функция f(x) называется непрерывной в точке x₀, если ее приращение в этой точке является бесконечно малой функцией при Dx ® 0.

19.2. Арифметические действия над непрерывными функциями.

Они приводят к тем же результатам, что и при рассмотрении пределов.

19.3. Непрерывность некоторых элементарных функций.

а) f(x) = C = const – проверить по определению.

б) f(x) = x – из определения.

в) xⁿ = x ×x × … × x – из теоремы о произведении непрерывных функций.

г) P(x) = C₀xⁿ + C₁x^n-1 + … + C_n

д) R(x) = …

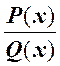q  R(x) = 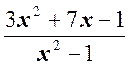 непрерывна во всех точках x Î R\ {–1; +1}.

е) sin x непрерывна в каждой точке x Î R.

 y = sin (x₀ + Dx) – sin x₀ = 2cos (x₀ + ) sin – это произведение ограниченной функции 2cos (x₀ + ) на бесконечно малую функцию sin  при Dx ® 0 и значит Dy ® 0 при Dx ® 0. Следовательно, sin x непрерывна в точке x₀, которая выбиралась произвольным образом.

ж) Непрерывность cos x, tg x, ctg x доказывается аналогично.

з) f(x) = |x|.

При x > 0 |x| = x и, значит, при всех таких значениях аргумента функция f(x) непрерывна, то же верно и в случае x < 0. В точке x = 0 нужно найти предел слева и справа, так как оба они равны 0, то есть равны f(0), то f(x) непрерывна и в нуле.

Важнейшим примером непрерывной функции является f(x) = a^x, 0 < a ¹ 1, однако доказательство непрерывности нужно разобрать самостоятельно.

Говорят, что f(x) непрерывна в интервале (a, b), если она непрерывна в каждой точке этого интервала; f(x) непрерывна во на отрезке [a, b], если она непрерывна во всех точках интервала (a, b), непрерывна в точке a справа и непрерывна в точке b слева.

19.4. Классификация точек разрыва функции.

Определение 3. Точка x₀ называется точкой разрыва функции f(x), если f(x) в (.) x₀ не является непрерывной.

Разрывы функции классифицируются следующим образом.

Разрыв 1-го рода. x₀ – точка разрыва первого рода функции f(x), если в этой точке функция f(x) имеет конечные, но не равные друг другу правый и левый пределы:

lim f(x)  ¹  lim f(x).

+1, при x > 0;

q    f(x) = sign x =       0, при x = 0;

–1, при x < 0.

lim f(x) = 1; lim f(x) = –1. 1 ¹ –1.

Разрыв 2-го рода. x₀ – точка разрыва 2-го рода, если в этой точке функция f(x) не имеет, по крайней мере, одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.

q  f(x) = . Точка O – точка разрыва 2-го рода функции f(x), так как lim = –¥, lim = +¥.

19.5. Кусочно-непрерывные функции.

Определение 4. f(x) – кусочно-непрерывная функция на отрезке [a, b], если она непрерывна во всех внутренних точках [a, b] за исключением, быть может, конечного числа точек, в которой она имеет разрыв 1-го рода, причем в точках a и b она имеет односторонние пределы.

Определение 5. Функция называется кусочно-непрерывной на всей числовой прямой, если она кусочно-непрерывна на каждом отрезке.

q  f(x) = [x] – кусочно-непрерывная на любом отрезке на R. [x] – целая часть x, то есть это наибольшее целое число не превосходящее x. При x = n (n Î Z) f(x) непрерывна справа и разрывна слева.

0