Определение ускорения свободного падения методом Бесселя, страница 2

График зависимости T1(x) и T2(x).

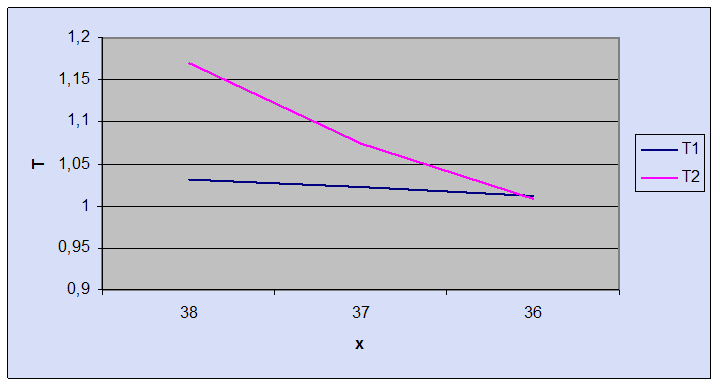
Таблица 2

№ измер	t1	Δt_i	Δt_i²	SΔt_i²	Δtсл	Δtпр	tср±Δt
1	21,357	-0,0368	0,00135424	0,106068563	0,296991976	0,001	21,3938±0,296993659
2	21,78	0,3862	0,14915044
3	21,236	-0,1578	0,02490084
4	21,173	-0,2208	0,04875264
5	21,423	0,0292	0,00085264
ср.зн.	21,3938		0,2250108	2,8	Δt=0,296993659
n	20
№ измер	t2
1	21,305	-0,007	0,000049	0,007231874	0,020249247	0,001	21,312±0,020273924
2	21,302	-0,01	0,0001
3	21,338	0,026	0,000676
4	21,317	0,005	0,000025
5	21,298	-0,014	0,000196
ср.зн.	21,312		0,001046	2,8	Δt=0,020273924
n	20

№ измер	T1	ΔT_i	ΔT_i²	SΔT_i²	ΔTсл	ΔTпр	Tср±ΔT
1	1,06785	-0,00184	0,00000324	0,005303486	0,014849761	0,001	1,06969±0,014883394
2	1,089	0,01931	0,000372876
3	1,0618	-0,00789	0,00006241
4	1,05865	-0,01104	0,000121882
5	1,07115	0,00146	0,00000213160
ср.зн.	1,06969		0,000562539	2,8	Δt=0,014883394
n	20
№ измер	T2
1	1,06525	-0,00035	0,0000001225	0,000361594	0,001012462	0,001	1,0656±0,001423053
2	1,0651	-0,0005	0,0000002500
3	1,0669	0,0013	0,0000016900
4	1,06585	0,00025	0,0000000625
5	1,0649	-0,0007	0,0000004900
ср.зн.	1,0656		0,0000026150	2,8	Δt=0,001423053
n	20

Таблица 3

L_ПР,м	31
l1,м	0,265
l2,м	0,045
T1,с	1,06969
T2, с	1,0656
g, м/с²	10,67893822

Вывод: рассчитав ускорение сводного падения по методу Бесселя и сравнив его с табличным значением; с учетом погрешностей, которые возникают за счет сил трения и сил сопротивления воздуха, можно сказать, что определение ускорения сводного падения по методу Бесселя является достаточно точным.

1 2

Скачать файл