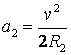Автоматизированное проектирование продольного профиля, страница 2

      ,                                                                           (4)

где v – скорость автомобиля.  Соответственно скачком будет изменяться и  центробежная сила, определяемая по формулам

                                      F₁=ma₁  и F₂=ma₂,

где m –масса автомобиля.

  Именно в этом проявляется    «неплавность» продольного профиля. При большой скорости движения автомобиля скачкообразные изменения центробежной силы  будут ощущаться в виде толчков.

Таким образом, плавность проектной линии, в принципе, невозможно обеспечить, применяя в качестве сопрягающего элемента круговые кривые или аппроксимирующие их квадратические параболы. При такой конструкции продольного профиля в точках сопряжения радиус вертикальной кривой всегда будет меняться скачком.

Чтобы обеспечить плавность проектной линии продольного профиля необходимо использовать кубические параболы. Тогда в пределах одного элемента радиусы будут плавно изменяться.

4  Проектная линия, построенная из кубических парабол

(кубических сплайнов)

Общее уравнение кубической параболы имеет вид:

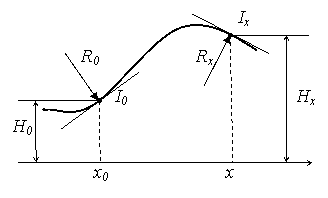
H(x)=H₀+x(I₀+x(C₀+xD)) .        (5)

Здесь H₀, I₀, C₀, D – коэффи-циенты, имеющие физический смысл:

H₀ – отметка проектной линии в начале элемента;

I₀   – уклон касательной к проектной линии в начале элемента;

C₀  – кривизна проектной линии в начале элемента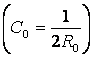или скорость изменения уклона;

D  – скорость изменения кривизны или ускорение изменения уклона проектной линии в пределах рассматриваемого элемента.

Если раскрыть скобки, то выражение (5) примет вид:

H(x)=H₀+I₀x+C₀ x²+D x³

Частными случаями функции (5) являются:

- квадратическая парабола – элемент с постоянной кривизной, т.е.                                             D=0:   

   H(x)= H₀+I₀x+C₀ x².                                                     (6)

Данная формула легко переходит в формулу  из метода Антонова. В самом деле, за начальную точку элемента принимаем вершину кривой. Как известно, в вершине I₀= 0‰, H₀=H_в. Тогда формула (6) перепишется в знакомом виде:

- прямой отрезок с нулевой кривизной, т.е. D=0 и C₀=0. Тогда выражение (5) примет вид:

                  H(x)=H₀+I₀x.                                                             (7)

Формула (7) лежит в основе метода тангенсов.

Таким образом, проектная линия, построенная из кубических парабол, является естественным обобщением известных ранее методов тангенсов и квадратических парабол (Антонова).

При конструировании проектной линии профиля круговыми кривыми (квадратическими параболами) принято, что отдельный конструктивный элемент – это либо выпуклая, либо вогнутая кривая. При использовании кубической параболы в отдельном конструктивном элементе, т.е. в пределах одной кривой может быть и вогнутая и выпуклая ветвь (а может быть и одна - выпуклая или вогнутая).