Автоматизированное проектирование плана трассы, страница 2

 

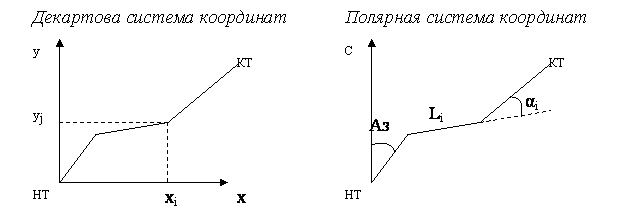
На следующем этапе проектировщиком задаются значения радиусов вписываемых кривых и длины переходных кривых. Результатом расчета являются две ведомости: ведомость углов поворота,  прямых и кривых и ведомость элементов трассы.

 Графический способ реализации метода тангенсов заключается в том, что на экран монитора выдается цифровая модель местности. С помощью курсора мыши фиксируются опорные точки полигонального хода и проводятся прямолинейные отрезки. После этого с помощью геометрического проектирования в углы поворота вписываются круговые кривые. Параметры закруглений, величины углов и ведомость углов поворота, прямых и кривых вычисляется автоматически.

Оба эти способа можно реализовать в программном комплексе CREDO.

3. Интерполирование линии трассы кубическими сплайнами

Применение ЭВМ породило совершенно новые методы построения плана трассы. В качестве математической линии трассы используются кубические сплайн-функции.

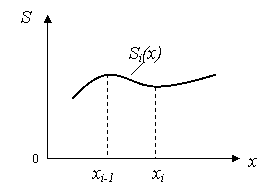Сплайнами называются функции, которые склеены из различных кусочков многочленов. В качестве таких многочленов взяты полиномы 3-й степени.

     S_i(x)=a_i(x-x_i)³+b_i(x-x_i)²+c_i(x-x_i)+d_i          (2)

при x_i-1  ≤ x ≤ x_i, i=1, 2 ,…, n.

      В точках сопряжения эти полиномы имеют общую касательную. Параметры a_i, b_i, c_i, d_i  называются коэффициентами сплайна, x_i, y_i – узлами сплайна.

       Сплайн моделирует старое инженерное приспособление – механический сплайн – упругую линейку. Если в точках сопряжения вбить гвоздики и между ними поместить тонкую металлическую линейку, то она изогнется по линии S. При этом ее потенциальная энергия будет минимальной. Из строительной механики известно, что условие минимума потенциальной энергии выражается уравнением

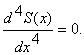                                                      (3)

Функция (2) как раз удовлетворяет данному условию.

Полученная аналитическая интерпретация эскизной линии трассы еще не дает возможности контроля за законами изменения кривизны линии. Для этого ее нужно перевести в обычную клотоидную трассу, т.е. представить её сочетанием элементов: отрезков, клотоид и круговых кривых.

Определим сначала длину трассы с помощью известных формул математического анализа

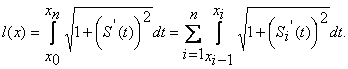                         (4)

Кривизна К, обратно пропорциональная величине радиуса, может быть вычислена по зависимости

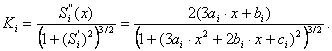                    (5)

Далее строится график кривизны. Затем он аппроксимируется ломаной линией.

  Проанализируем данный график.

    1) На первом участке ломаной К=0, т.е. 1/К=∞. Это соответствует прямо-линейному участку трассы.

     2) На втором участке К=const≠0. Это означает, что R=const. Это соответствует круговой кривой.

3) На третьем участке кривизна пропорциональна длине трассы, т.е. радиус обратно пропорционален длине трассы. Такая зависимость имеет место в уравнении (1) для клотоиды. Таким образом, наклонные участки в ломаной линии моделируются клотоидой.

Существенным недостатком интерполирования эскизной линии кубическими сплайнами является то, что их очертания сильно зависят от положения узлов интерполяции эскизной линии. Сама же процедура назначения местоположения узлов плохо формализуется, что сильно снижает возможность применения интерполяционных сплайнов для трассирования дорог. Более эффективным и универсальным аппаратом трассирования являются сглаживающие сплайны.