Неинерциальные системы отсчета. Абсолютное, относительное и переносное движения. Кориолисово и осестремительное ускорения. Силы инерции. Уравнение динамики в НИСО

ТЕМА 13 НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА

1 Абсолютное, относительное и переносное движения.

2 Кориолисово и осестремительное ускорения.

3 Силы инерции.

4 Уравнение динамики в НИСО.

Вопросы для самоподготовки

1 Что понимают под абсолютным, относительным и переносным движением?

2 Какие системы отсчета называются неинерциальными? В чем их принципиальное отличие от инерциальных систем отсчета?

3 Какой системой отсчета является система отсчета связанная с Землей?

4 Что такое силы инерции? Каковы их особенности?

5 Назовите силы инерции. Какие из них являются консервативными, диссипативными?

6 Выполняется ли закон сохранения импульса в неинерциальных системах отсчета?

7 Чему равен момент центробежной  силы относительно оси, вокруг которой вращается система отсчета?

8 На диске, вращающемся с постоянной угловой скоростью  покоится тело массы m. Расстояние тела от оси вращения R. Какие силы действуют на тело в неподвижной системе отсчета? В какой системе отсчета к предыдущим силам добавиться только центробежная сила инерции? В какой системе отсчета появится еще и сила Кориолиса?

Основные понятия по теме

В неинерциальных системах отсчета законы Ньютона, а следовательно и все законы классической механики, справедливы в предположении, что кроме сил взаимодействия с другими телами действуют силы инерции, не обусловленные взаимодействием. Силы инерции зависят, прежде всего, от характера движения неинерциальной системы отсчета. Это значит, что для нахождения сил инерции необходимо знать, как движется неинерциальная система относительно инерциальной системы, то есть знать характер движения, его кинематические параметры.

В системе отсчета, движущейся относительно какой-либо инерциальной системы поступательно и прямолинейно с ускорением , на тело действует сила инерции

                                                          (13.1)

В системе отсчета, вращающегося с постоянной угловой скоростью  относительно какой-либо инерциальной системы, действуют центробежная сила инерции

                                                         (13.2)

и сила Кориолиса

                                                      (13.3)

где радиус-вектор, проведенный от оси вращения к центру масс тела, скорость тела относительно вращающейся неинерциальной системы.

Уравнение динамики в неинерциальной системе отсчета, которая вращается с постоянной угловой скоростью  вокруг неподвижной оси,

                                         (13.4)

В общем случае уравнение аналогичное (13.4) имеет вид

                                    (13.5)

Здесь равнодействующая внешних сил, приложенных к телу.

Примеры решения задач

1 На грань клина, образующего угол α = 60° с горизонтом, положили небольшое тело. Коэффициент трения между телом и клином  С каким минимальным (максимальным) ускорением нужно двигать клин в горизонтальном направлении, чтобы тело не скользило относительно клина?

 

   Решение. Задачу удобно решать в системе отсчета связанной с клином. Такая система отсчета будет неинерциальной и в ней, наряду с традиционными силами тяжести , реакции клина  и трения  (рисунок 13.1), будет присутствовать сила инерции , направленная в сторону, противоположную

движению клина. Из условия неподвижности тела относительно клина:

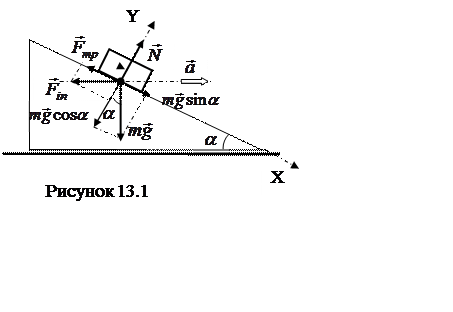
                                            (1)

ясно, что направление  должно быть таким, чтобы ее составляющая была направлена вверх вдоль грани клина. Только в этом случае она позволит скомпенсировать результирующую силы трения  и составляющей силы тяжести .

В проекциях на оси OX и OY для двух возможных случаев направления силы трения, условие (1) приводит к системе уравнений:

 направлена вверх (на рисунке ___ показан именно этот случай):

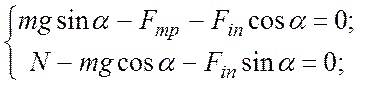                               (2)

 направлена вниз:

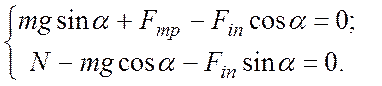                               (3)

Учитывая, что , где m – масса тела, и решая системы уравнений (2) и (3), находим, что в первом случае ускорение клина по модулю равно

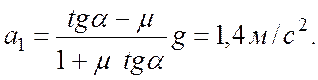
Во втором случае

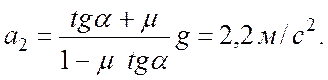
Причина, по которой оказалось, что , будет ясна читателю, если он изобразит аналог рисунка 13.1 для второго случая.

2 На сколько будут отличаться конечные скорости разбега самолета, если самолет взлетает на экваторе, причем один раз его разбег производится с запада на восток, а второй с востока на запад. Подъемная сила, действующая на крылья самолета, пропорциональна квадрату его скорости относительно Земли  ~ Необходимая конечная скорость разбега самолета вдоль меридиана равна .

Решение. В неинерциальной системе отсчета, связанной с Землей, на самолет действуют силы: сила тяжести, подъемная сила, центробежная сила, сила Кориолиса. Схематически направление сил в трех рассматриваемых в условии задачи случаях показано на рисунках 13.2 а), б), в):