Компьютерное моделирование опыта Штерна-Герлаха, изучение поведения атомов в неоднородном магнитном поле, измерение магнитного момента атомов, страница 3

В дальнейшем Штерн и Герлах значительно усовершенствовали свою установку и методику измерений. В частности, был применен более чувствительный метод регистрации пучка, использующий механизм поверхностной ионизации атомов щелочных металлов на раскаленной нити детектора. Это позволило измерить величину проекции магнитного момента атома лития, которая оказалась равной одному магнетону Бора. Систематические исследования различных элементов дали результаты, находящиеся в полном согласии с теорией.

В 1933 году О. Штерн с помощью своего метода в эксперименте с пучком молекулярного водорода впервые измерил магнитный момент протона, а затем и магнитный момент дейтрона. Результат опыта стал научной сенсацией: магнитный момент протона оказался почти в три раза больше, чем предсказывала теория. За основополагающий вклад в развитие метода молекулярных пучков и измерение магнитного момента протона О. Штерн был удостоен в 1943 г. Нобелевской премии. Позже американский физик И. Раби и его сотрудники в значительной мере улучшили методику измерения ядерных магнитных моментов, соединив метод молекулярных пучков и явление магнитного резонанса.

Опыт Штерна – Герлаха сыграл важную роль и для подтверждения основного принципа квантовой механики – принципа суперпозиции.

8.4. Влияние распределения атомов по скоростям
на расщепление пучка

При оценке ожидаемого отклонения атомного пучка удвоенная кинетическая энергия атомов приравнивалась к  3 kT

,

(8.12)

и предполагалось, что пучок состоит из атомов с одной и той же скоростью. В действительности же, поскольку пучок получается испарением вещества, атомы в нем характеризуются некоторым распределением по скоростям. Если учесть, что согласно (8.11) величина отклонения атома прямо пропорциональна проекции магнитного момента μ_z  и обратно пропорциональна квадрату скорости атома, то при  m_J = –1/2, +1/2 каждая из двух полосок на пластинке должна несколько размыться, но в центральной части все-таки останется минимум. При этом размывание каждой полоски является асимметричным: в направлении от центра – большим, а в направлении к центру – меньшим. Действительно, для паров серебра, находящихся в печи, выполняется распределение Максвелла

,

где – относительное число атомов, имеющих скорость от v до  v + dv, k – постоянная Больцмана, T – абсолютная температура. В то же время   – число атомов (со скоростями от vдо v+dv), проходящих за единицу времени сквозь отверстие и образующих пучок, пропорционально  vּdNи следовательно:

.

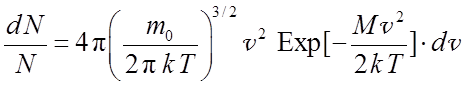(8.12)

Выразим из (8.11) скорость  vкак функциюz

(8.13)

где  , и свяжем промежуток  dzна пластинке, с интервалом  dv скоростей атомов, попавших в этот промежуток:

.

(8.14)

Подставляя  dv из (8.14) и  v(z)  из (8.13) в соотношение (8.12), получим для плотности осевших на пластинку атомов искомое асимметричное распределение:

.

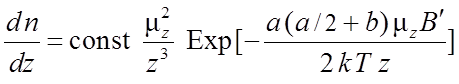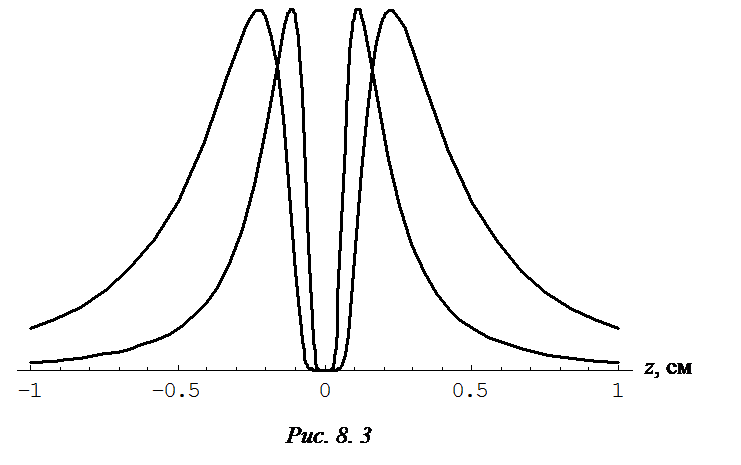
На рис. 8.3 изображены графики распределения плотности  серебра на пластинке как функции z , при  a =10 см, b =15 см, для температур 1000 К  и  2000 К.

С другой стороны, в классическом случае интенсивность единственной сильно размытой полосы имела бы максимум в центре картины. Таким образом, различие между квантовым и классическим случаями при m_J = –1/2, +1/2 является совершенно четким. Благодаря этому опыт Штерна – Герлаха с атомами серебра оказался успешным.