Кинематика относительного движения. Осестремительное и кориолисово ускорения. Относительная скорость движения двух материальных точек

ТЕМА 3 КИНЕМАТИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ

1 Абсолютное, относительное и переносное движения.

2 Осестремительное и кориолисово ускорения.

.    3 Относительная скорость движения двух материальных точек.

Вопросы для самоподготовки

1 Что понимают под абсолютным, относительным и переносным движением?

2 Какой вид примут соотношения (3.1)  ̶  (3.3) в случае, когда системы отсчета К и  инерциальные?

3 Какими факторами обусловлены составляющие переносного ускорения в общем случае движения системы ?

4 Что общего и каковы отличия в ориентации осестремительного и кориолисова ускорений относительно оси вращения системы ?

5 Как найти относительную скорость движения двух материальных точек? Чем отличаются относительные скорости  и  материальных точек 1 и 2?

Основные понятия по теме

Рассмотрим движение материальной точки М относительно двух систем отсчета: неподвижной системы отсчета  и движущейся относительно системы  системы . Будем считать, что начало  системы  совершает произвольное движение, а сама эта система вращается с постоянной угловой скоростью  (рисунок 3.1).

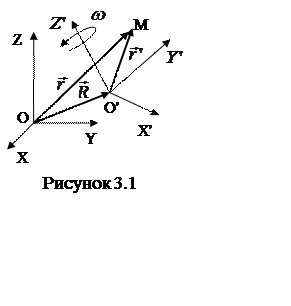В механике движение точки М относительно системы  и относительно системы  называют абсолютным и относительным движением соответственно. Движение системы  относительно системы  называется переносным движением.

Пусть   и  радиус-вектор, скорость и ускорение точки М при ее абсолютном движении.       и        ̶      аналогичные  

величины, характеризующие относительное движение точки М. Радиус-вектор, скорость и ускорение начала отсчета  подвижной системы  по отношению к неподвижной системе  обозначим через   и . Тогда кинематические соотношения между перечисленными величинами имеют вид

                                                     (3.1)

                                         (3.2)

                     (3.3)

Выражения (3.2) и (3.3) упрощаются в следующих частных случаях:

     ̶  при поступательном движении системы , когда , из (3.2) и (3.3) получаем

                                                    (3.4)

                                                    (3.5)

̶  если материальная точка М жестко связана с движущейся системой

отсчета , то есть  то

                                              (3.6)

                                      (3.7)

В этом случае ускорение  называют переносным ускорением. Как ясно из (3.7), переносное ускорение обусловлено как движением начала отсчета системы , так и ее вращением.

Второе слагаемое в формуле (3.7) можно преобразовать к виду

                                            (3.8)

где составляющая радиус вектора  точки М, перпендикулярная вектору  Вектор  направлен от точки М к оси вращения движущейся системы .В связи с этим второе слагаемое в (3.7) принято называть осестремительным ускорением.

Последнее слагаемое в формуле (3.3)

                                                 (3.9)

называют кориолисовым ускорением. Кориолисово ускорение отлично от  нуля только для точки, движущейся относительно вращающейся системы отсчета.

Учитывая (3.7) и (3.9), формулу (3.3) можно переписать в виде

                                         (3.10)

Таким образом , в общем случае абсолютное ускорение материальной точки равно сумме относительного, переносного и кориолисова ускорений.

В заключение рассмотрим вопрос об относительной скорости движения двух материальных точек. Пусть  и  абсолютные скорости точек 1 и 2 относительно некоторой системы отсчета .Связав начало  движущейся системы отсчета  с точкой 2, для скорости абсолютного движения точки 1 согласно (3.4) можем записать

где скорость движения точки 1 в системе

Отсюда следует, что

                                         (3.11)

то есть скорость движения точки 1 относительно точки 2 равна разности скоростей абсолютного движения этих точек.

Примеры решения задач

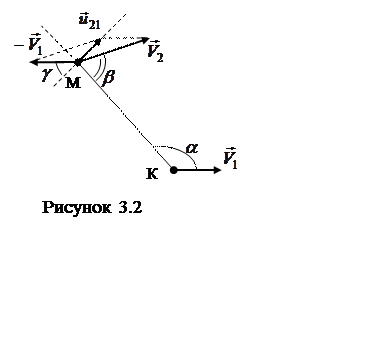1 Катер К, движущийся со скоростью , тянет за собой лыжника М на водных лыжах. В некоторый момент времени скорость катера  и неизвестная скорость лыжника  образуют с фалом углы  и  соответственно (рисунок 3.2). Определите скорость лыжника относительно катера в этот момент времени.

Решение. В системе отсчета связанной с катером лыжник в каждый момент времени будет   двигаться   по   окружности,   центр

которой совпадает с катером, а радиус равен длине фала. Следовательно, вектор искомой относительной скорости

                                                     (1)

будет ориентирован перпендикулярно фалу (рисунок 3.2).

Спроектировав выражение (1) на направления ориентированные вдоль фала и перпендикулярно ему, получаем

                                              (2)

                                            (3)

где угол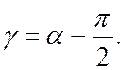

Решая систему уравнений (2) и (3) относительно неизвестных  и , находим

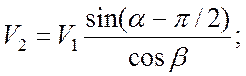
              (4)

В заключение заметим, что дальнейшие преобразования выражений (4) являются нецелесообразными, так как при заданных углах  и  значения всех тригонометрических функций входящих в эти выражения положительны.

2 Автомобиль А движется по дуге окружности радиуса , а автомобиль В  ̶  прямолинейно. Скорость каждого автомобиля постоянна и равна  В некоторый момент времени автомобили занимают положения изображенные на рисунке 3.3. Определите скорость автомобиля В относительно автомобиля А в этот момент, если расстояние между ними равно

Решение. С точки зрения водителя автомобиля А все окружающее пространство вращается вокруг точки О, являющейся центром окружности по дуге которой он движется, с угловой скоростью 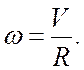 Тогда, если бы автомобиль В покоился, его скорость относительно автомобиля А была бы равна

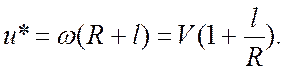
Для заданного положения автомобилей скорость  направлена так, как показано на рисунке 3.3.