Исследование сложной цепи постоянного тока (Лабораторная работа № 3)

Лабораторная работа № 3

Исследование сложной цепи постоянного тока

    Цель работы:

-  освоить методы расчета токов в ветвях разветвленной схемы постоянного тока (законы Кирхгофа, метод контурных токов, метод наложения);

-  освоить методику расчета узловых потенциалов и построения потенциальной диаграммы;

-  приобрести навыки по измерению постоянных напряжений и токов в электрической цепи;

         Продолжительность работы – 4 часа.

1 Сведения из теории. Методы общего анализа линейных электрических цепей с несколькими источниками

     1.1 Метод расчета электрических цепей с применением   правил Кирхгофа

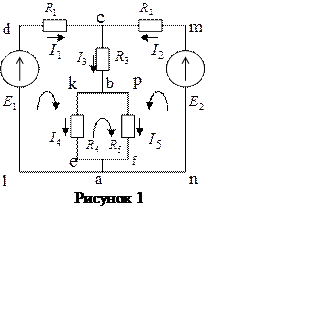
    Рассмотрим сложную электрическую цепь (рис. 1). Порядок расчета следующий:

- произвольно указываем направление  токов во всех ветвях. Если принятое направление тока не совпадает с действительным, то  при расчете такие токи получаются со знаком минус;

- составляют (N – 1) уравнение по первому правилу Кирхгофа, где N – число узлов;

- недостающие уравнения в количестве М – (N – 1), где М – число ветвей, составляем по второму правилу Кирхгофа, при этом обход контура можно производить как по часовой  стрелке, так и против нее. При этом все э.д.с., направления которых совпадает с направлением обхода контура, записываются со знаком плюс, а все э.д.с., направление которых противоположно – со знаком минус. Направление действия э.д.с. внутри источника всегда принимают от минуса к плюсу;

- число составленных уравнений по первому и второму правилам Кирхгофа должно быть равно числу неизвестных токов;

- полученную систему уравнений решают относительно неизвестных токов.

    Составим расчетное уравнение для электрической цепи, изображенной на рис. 1 выбрав произвольно направления токов в ветвях цепи, составляем уравнения по первому правилу Кирхгофа для узлов с и в:

                                                       

    Выбрав направления обхода контура, составляем уравнения по второму правилу Кирхгофа для трех произвольно выбранных контуров:

 

для контура a e k b c d:  

для контура a f p b c m n:     

для контура e k b f:        

    Решаем совместно записанные уравнения, определяем токи в ветвях электрической цепи.

1.2 Метод расчета электрических цепей с применением контурных токов

    Метод заключается в том, что вместо действительных токов в ветвях на основании второго правила Кирхгофа определяются так называемые контурные токи. Контурным называется такой расчетный ток, который замыкается только по своему контуру, оставаясь вдоль него неизменным. Согласно этому методу, действительный ток в любой ветви, принадлежащий только одному контуру, численно равен контурному току, а в ветви принадлежащей нескольким контурам, равен алгебраической сумме контурных токов, приходящих через эту ветвь.

    Число уравнений, составленных по второму правилу Кирхгофа, в этом случае равно числу независимых контуров. Контур считается независимым, если в каждом из них имеется хотя бы одна ветвь, не принадлежащая другим контурам. Число независимых контуров определяется так M - (N - 1), где М – число ветвей, N – число узлов. Составляя уравнения по второму закону Кирхгофа для контурных токов, принято сумму сопротивлений, входящих в контур, называть собственным сопротивлением, а сопротивления принадлежащие одновременно двум или нескольким контурам – общим сопротивлением. Направление обхода контура выбирают произвольно. Обычно принимают совпадающим с направлением контурного тока. Значение э.д.с. берется со знаком плюс, если направление обхода контура совпадают с положительным направлением э.д.с. и со знаком минус, если не совпадает.

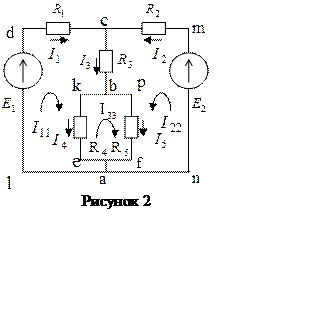
    Рассмотрим схему, изображаемую на рисунке 2. Составим для нее уравнение  по методу контурных токов:

для контура a k b c d l: 

для контура a p b c m n: 

для контура а k b р:     

где:  

              

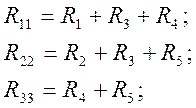
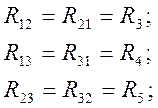
    Уравнение можно записать сразу и в таком виде:

                                     

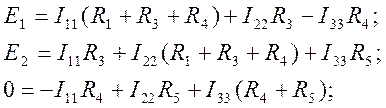
   Решая совместно уравнения, определяем контурные токи. В том случае, когда контурный ток получается со знаком минус, это означает, что его направление противоположно помеченному на схеме. Зная контурные токи, определяем действительные токи. В данной задаче они определяются следующим образом.

1.3 Метод расчета электрических цепей с применением метода наложения

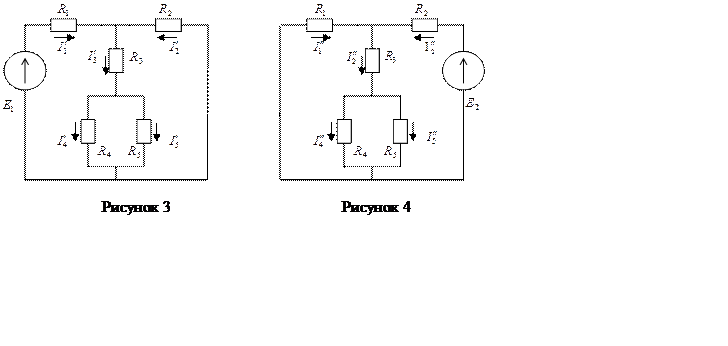
    Этот метод применим только в линейных электрических цепях, в которых сопротивления элементов цепи не изменяются при прохождении  через них тока или приложенного к ним напряжения. Расчет  основывается на том, что в ветвях цепи определяют токи от действия  каждого источника в отдельности (частичные токи), а затем действительные токи определяются как алгебраическая сумма частичных токов. Рассмотрим схему рисунка 1. Исключим в ней источник Е₂ (Е₂ = 0). Тогда схема имеет вид рисунка 3.

    Ток в разветвленной части цепи определим как

    ;       

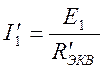где                              ;      

                                       

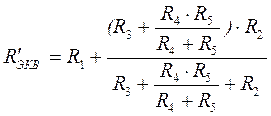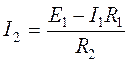
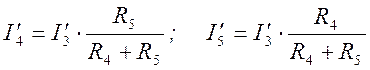
    Исключим Е₁ (Е₁ = 0). Тогда схема имеет вид указанный на рисунке 4. Ток в неразветвленной части цепи определим как:

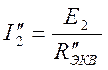
где                               ;

;       

;     .

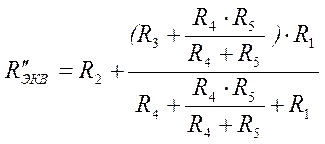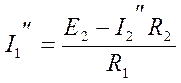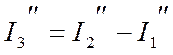
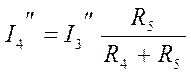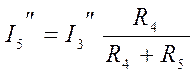    Действительные токи, согласно выбранных направлений рисунке 1 определим как алгебраическую сумму частичных токов.

1.4 Потенциальная диаграмма

    Для анализа работы электрических цепей и улучшения режимов их работы, особенно в схемах электроники, важно знать распределение потенциала в цепи. Графическое изображение распределения потенциала в электрической цепи называется потенциальной диаграммой.