Изучение вынужденных колебаний (Лабораторная работа № 11)

ЛАБОРАТОРНАЯ РАБОТА №11

ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ

ЛАБОРАТОРНАЯ РАБОТА №11

ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ

Цель работы: получить вынужденные колебания .возникающие в колебательном контуре

под воздействием внешней Э.Д.С., изучить явления, наблюдаемые при внешних возбуждениях колебаний с частотами, близкими к резонансной и исследовать зависимость амплитуды и фазы этих колебаний от частоты вынуждающего воздействия.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Рассмотрим электрическую цепь, содержащую активное сопротивление R, конденсатор емкости С, .катушку индуктивности L и источник напряжения U (рис. 11.1).

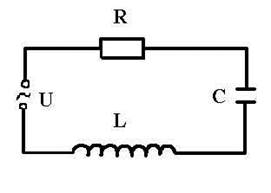
Рисунок 11.1

В соответствии со вторым законом Кирхгофа полная Э.Д.С., действующая в цепи, равна сумме падений напряжения на всех участках цепи

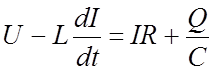            (11.1)

Здесь  - Э.Д.С. самоиндукции, возникающая в .катушке, Ua.=IR падение напряжения на активном сопротивлении, U_c=Q/C разность потенциалов между обкладками конденсатора. Дифференцируя уравнение (11.1) по времени и учитывая, что dQ/dt=I, получим:

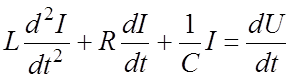           (11.2)

Наибольший интерес представляет анализ, гармонического переменного тока, поскольку с помощью преобразования Фурье произвольный ток может быть представлен в виде совокупности гармонических составляющих. Для удобства дифференцирования силу тока и напряжение в цепи представим в комплексной форме

,

где I₀ и U₀ некоторые комплексные числа. При этом необходимо иметь в виду, что ток и напряжение, как реальные физические величины, должны описываться действительной частью выражений (11.3). Поэтому после выполнения преобразований согласно (11.2) в найденных решениях необходимо выделить действительную часть. Поскольку уравнении (11.2) является линейным, то окончательный результат будет таким же, как и в случае выполнения преобразования только над действительной частью выражений (11.3). Подставляя (11.3) в уравнение (11.2), после дифференцирования получаем:

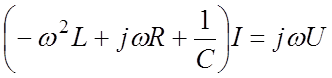    (11.4)

Разделив обе части уравнения на , eгo можно представить в виде:

          (11.5)

выражающем законом Ома для цепи переменного тока. Комплексная величина

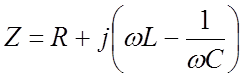       (11.6)

называется импедансом он играет роль сопротивления цепи, зависящего от частоты тока w. Импеданс характеризует соотношение между амплитудами и фазами тока и напряжения в цеп и, содержащей активное сопротивление, емкость и индуктивность.

Зависимость между током и напряжением (11.5) можно проиллюстрировать графически путем проставления комплексных величин векторами на комплексной плоскости. При этом гармонически изменяющаяся величина изображается вектором, вращающегося с частотой w вокруг начала координат против часовой стрелки. Длина вектора равна амплитуде колебаний рассматриваемой физической величины, а угол между вектором и осью ОХ равен фазе колебаний. Совместим ось ОX с вектором силы тока I в произвольный момент времени (рис 11.3), тогда вектор падения напряжения на активном сопротивлении U_а=IR также будет направлен вдоль оси. Падение напряжения на катушке и конденсаторе соответственно равно

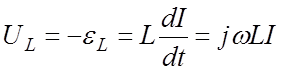            (11.7)

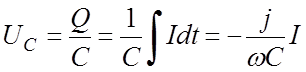        (11.8)

При определении ориентации векторов U_L и U_C необходимо учесть, что согласно формуле Эйлера, 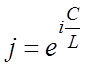. Следовательно, умножение произвольной комплексной величины  на  эквивалентно повороту вектора на комплексной плоскости на угол 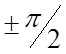 без изменения длины этого вектора:

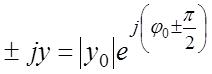                        (11.9)

В соответствии с этим правилом, напряжение на катушке (11.7) всегда опережает по фазе силу тока на 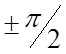, а напряжение на конденсаторе (11.8) отстает по фазе от силы тока на 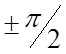. Построив на комплексной плоскости векторы U_L и U_c ,можно графически определить полное напряжение как сумму падений напряжения на всех участках цепи.

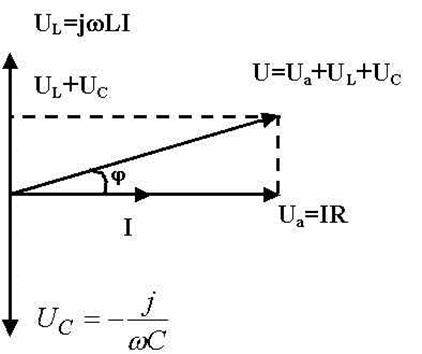
Рисунок 11.2

Векторная диаграмма цепи рис.(11.2), показывает, что полное напряженна U, может, как опережать по фазе силу тока, так и отставать от нее. При этом сдвиг фаз между током и напряжением в цепи определяется выражением

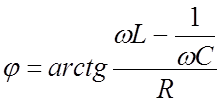          (11.10)

а амплитуда напряжения и силы тока связаны соотношением:

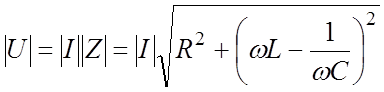       (11.11)

Формула (11.10) показывает, что сдвиг фаз между током и напряжением может принимать как положительные, так и отрицательные значения в зависимости от соотношения параметров цепи и частоты тока. Для частоты тока 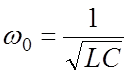 совпадающей с собственной частотой колебательно контура, сдвиг фаз j равен нулю. В этом случае напряжения на конденсаторе и катушке взаимно компенсируются (они равны по величине, но противоположны по знаку .поскольку имеют относительно друг друга сдвиг фаз, равный p). Сила тока такая же, как при отсутствии в цепи реактивных элементов, то есть принимает максимальное значение |I|=|U|/R (в последовательной цепи имеет место резонанс напряжений).

Сдвиг фаз между током и напряжением в цепи переменного тока можно определить с помощью электронного осциллографа. Допустим необходимо измерить сдвиг фаз между двумя гармоническими сигналами одинаковой частоты. Подадим эти сигналы на горизонтально и вертикально отклоняющие пластины осциллографа тогда смещения электронного луча по горизонтали и вертикали будут изменяться с течением времени следующим образом: