Изучение затухающих колебаний (Лабораторная работа № 10)

Лабораторная работа №10

Изучение затухающих колебаний.

Цель работы: исследование свободных затухающих колебаний, измерение и расчёт их характеристик.

Теоретические сведения.

Электромагнитные колебания в RLC-контуре в отсутствие внешнего напряжения можно описать с помощью дифференциального уравнения для силы тока

L*(d²I/dt²)+R*(dI/dt)+(1/C)*I=0

Вводя собственную частоту колебаний W₀=Ö I/LC   и коэффициент затухания γ=R/2L, перепишем уравнение в виде I+2γI+W₀²I=0

Решая это уравнение, можно показать, что в зависимости от соотношения между параметрами W₀ и γ возможны следующие типы колебаний в контуре:

А) затухающие колебания,  которые имеют место в случае        W₀²_-γ²>0. При этом зависимость силы тока от времени имеет вид

I=I₀ e^-γt cos(wt+δ), где w=Öw₀²-γ² -частота, δ-начальная фаза колебаний,   I₀-их начальная амплитуда. (рис .10.1.а.)

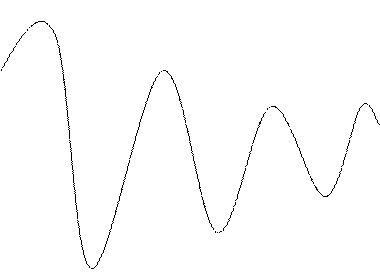
                                                                                           Величина δ и I₀ могут быть

I₁                                    определены из начальных условий.

I₂                        Для характеристики затухающих колебаний, вводятся также такие  

t₁                                      величины, как период колебаний

t₂                         T=2π/w =2π [1/LC-(R/2L)²] ^–1/2

                                                                                    логарифмический декремент                

рис10.1.а.                                                      затухания

d=lnI₁/I₂=γT=nR[L/C-R²/4] _–1/2, и добротность контура  Q=π/d

Здесь I1 и I2 – значения силы тока в моменты времени t1 и t2=t1+T,

Отстоящие друг от друга на один период колебаний.

Б)  апериодическое затухание  силы тока в контуре, которое наблюдается в случае w₀²-γ²<0  . При этом сила тока монотонно убывает  до нуля по закону  I=Ae^-α1t+Be^-α2t , где α₁₂=γ+-      , А и В величины определяемые из начальных условий(рис.10.1.б)

I

 

                                                                                                                                                                       

                                                                       t

 

            рис.10.1.б.

в) критический режим изменение силы тока, который имеет место при выполнении соотношения  w₀²-γ²=0 и представляет собой придельный случай рассмотренных выше затухающих колебаний и апериодического режима. При этом зависимость силы тока от времени можно записать в виде

                   I=(A+Bt)e ^–γt, где значения постоянных А и В определяется из начальных условий. График зависимости  в случае А= 0, В=0  и А=0 , В=0 представлен на (рис10.1.в.)

 

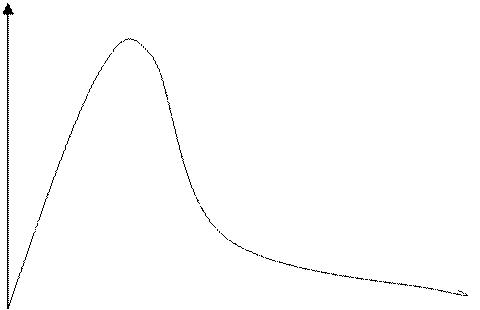
                     А=0    

В=0

Рис.10.1.в.                                     

Сопротивление Rкр=2√L/C, при котором выполняется соотношение

w₀²-γ²=0, называется критическим сопротивлением.

Если колебательный процесс изучать в системе координат  I-U, где I-ток в контуре,  U- напряжение на конденсаторе, то плоскость I-U называется фазовой плоскостью,  а кривую изображающую такую зависимость, называют фазовой кривой (рис.10.2.)

U

                    U₀

При затухающих колебаниях              

                                                       амплитуда напряжения и силы               

                             I    тока в контуре убывает, а фазовая кривая превращается в спираль, приближающаяся к фокусу 0.При

R>=Rкр колебательный процесс прекращается и спираль пирвращается в окружность, кривую.

Приборы и принадлежности.

Кассета ФПЭ-10/11, кассета ФПЭ-09/ПИ, магазин сопротивлений, источник питания, генератор, осциллограф.

Описание установки.

Принцип работы кассеты ФПЭ-10 основан на получении затухающих колебаний в колебательном контуре L₁,C₁, соединенных через гнёзда Х₅-Х₆  с магазинным сопротивлением   (0-1000 Ом), во время паузы подаваемых через гнёзда Х₁-Х₂ прямоугольных импульсов. Вспомогательные элементы R₁,VD₁ ограничивают амплитуду напряжения в момент подачи импульса. Колебания в контуре наблюдаются и изучаются с помощью осциллографа , подключаемого к гнёздам Х₃-Х₄-Х₇ (рис.10.3.а)