Цель: усвоение понятия электрической емкости, изучение процессов зарядки и разрядки конденсатора осциллографическим методом, определение времени релаксации процесса и емкости конденсатора.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
 Если подключить конденсатор к источнику постоянного тока (рис 8.1),
то напряжение на нем Uc экспоненциально
возрастает, асимптотически стремясь к ЭДС источника. При этом ток I (см. направление тока на рис 8.1), протекающий через
сопротивление R, убывает по экспоненте, уменьшаясь до
нуля.
Если подключить конденсатор к источнику постоянного тока (рис 8.1),
то напряжение на нем Uc экспоненциально
возрастает, асимптотически стремясь к ЭДС источника. При этом ток I (см. направление тока на рис 8.1), протекающий через
сопротивление R, убывает по экспоненте, уменьшаясь до
нуля.
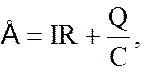 Процесс зарядки конденсатора можно
описать с помощью закона Ома для полной цепи:
Процесс зарядки конденсатора можно
описать с помощью закона Ома для полной цепи:
(8.1)
согласно которому сторонняя ЭДС равна сумме падений напряжения на всех участках цепи (внутренним сопротивлением источника пренебрегаем). В выражении (8.1) учтено, что напряжение Uc на обкладках конденсатора связано с зарядом Q соотношением Uc = Q/C , где С – емкость конденсатора. Дифференцируя (8.1) по времени и принимая во внимание, что сила тока равна скорости изменения заряда на обкладках
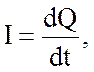 |
получаем дифференциальное уравнение с разделяющимися переменными
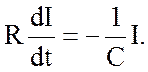 |
(8.2)
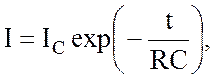 Решение уравнения (8.2) имеет
вид:
Решение уравнения (8.2) имеет
вид:
(8.3)
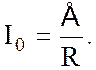 где постоянная интегрирования IC , равная
силе тока в момент времени t=0, может быть определена из начальных условий.
Поскольку в начальный момент времени Q=0, (заряд на обкладках не
успел накопиться), то из (8.1) следует:
где постоянная интегрирования IC , равная
силе тока в момент времени t=0, может быть определена из начальных условий.
Поскольку в начальный момент времени Q=0, (заряд на обкладках не
успел накопиться), то из (8.1) следует:
(8.4)
При разрядке конденсатора соответственно справедливы соотношения
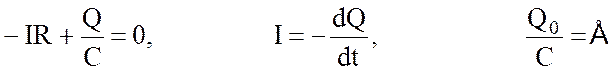 |
(направление тока изменилось на противоположное, происходит уменьшение заряда на обкладках, начальное напряжение на конденсаторе равно ЭДС источника). В результате зависимость силы тока от времени остается неизменной.
Из уравнения (8.3) находим закон изменения напряжения UR на сопротивлении R и напряжения на конденсаторе UC (рис 8.2):
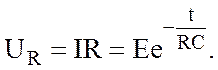 |
(8.5)
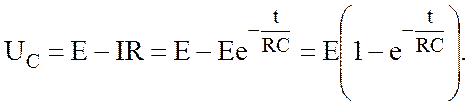 |
(8.6)
 |
![]() Для характеристики средней
скорости изменения силы тока в цепи при зарядке и разрядке конденсатора
вводится в рассмотрение время релаксации системы:
Для характеристики средней
скорости изменения силы тока в цепи при зарядке и разрядке конденсатора
вводится в рассмотрение время релаксации системы:
(8.7)
в течение которого сила тока
уменьшается в е раз, т.е. при t = t составляет 0,368 от
максимального значения 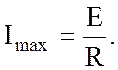
Закон изменения тока I и напряжений UR и UC при разрядке конденсатора через сопротивление R при отключенной ЭДС. Е находится из уравнения UС = IR. Студентам самим предоставляется возможность выполнить решение этой задачи и убедиться в том, что UС , I и UR при разрядке конденсатора изменяются по одному и тому же закону: ~exp(-t/RC). Если прологарифмировать выражение (8.3), получаем:
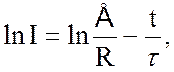 |
(8.8)
то есть изменение логарифма силы тока прямо пропорционально времени. При этом угловой коэффициент прямой, графически выражающий зависимость ln I =f(t), связан со временем релаксации обратной зависимостью
tg a = 1/t. Точка пересечения прямой с осью ординат дает значение логарифма начальной силы тока (рис 8.3).

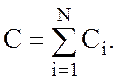 На практике часто используется параллельное
или последовательное соединение конденсаторов. Емкость нескольких параллельно
соединенных конденсаторов равна сумме их емкостей:
На практике часто используется параллельное
или последовательное соединение конденсаторов. Емкость нескольких параллельно
соединенных конденсаторов равна сумме их емкостей:
В случае последовательного соединения конденсаторов справедлива такая же формула, как при параллельном соединении резисторов:
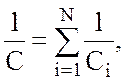
где N – количество соединенных конденсаторов.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ.
Кассета ФПЭ–ПИ/09, магазин сопротивлений (2шт), магазин емкостей, источник питания, генератор низкочастотный, осциллограф С1-117.
ОПИСАНИЕ УСТАНОВКИ.
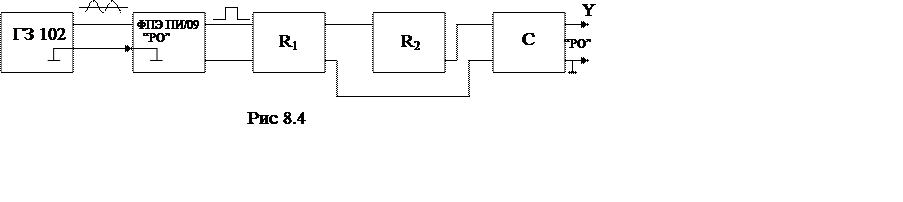 |
С низкочастотного генератора синусоидальный сигнал подается на кассету ПИ, с выхода которой прямоугольные импульсы через два магазина сопротивлений подаются на магазин емкостей. Для того, чтобы получить осциллограммы зарядки и разрядки конденсатора, необходимо через постоянные промежутки времени подключать конденсатор к цепи и сразу же его отключать. При чем частота переключения должна быть такой, при которой незаметно было бы мерцание изображения на экране. Роль такого переключателя в данной работе выполняют прямоугольные импульсы, получаемые с помощью кассеты ФПЭ–ПИ/09 или непосредственно с выхода генератора, поскольку большинство генераторов имеют синусоидальный и прямоугольный выходной сигналы.
Синусоидальный сигнал (1-3)В подается от входных гнезд Х1, Х2 через разделительный конденсатор С1 на компоратор напряжения (микросхема серии К554СА3Б). Выходной сигнал компоратора управляется усилительным каскадом. С выходных гнезд Х3, Х4 снимается сигнал прямоугольной формы положительной полярности, амплитудой 11,5 В при нажатой кнопке S 2.2. При нажатии кнопки S 2.1 переключателя S2 (см переднюю панель кассеты ФПЭ–ПИ/09) на выходе получаем сигнал синусоидальной формы. К кнопке S 2.3 подпаян диод, препятствующий разряду емкости через преобразователь импульсов в период паузы. Плавное изменение скважности осуществляется изменением активного сопротивления потенциометром R1, глубокая регулировка скважности осуществляется при помощи кнопочного переключателя S1, установленного на передней панели. Этим переключателем можно менять емкость цепочки, подключив один конденсатор С2 или оба сразу С2 и С3.
ВЫПОЛНЕНИЕ РАБОТЫ.
1. Используя рис 8.4 соберите рабочую схему. Подключите к разъему кассеты ФПЭ–ПИ/09 кабель источника питания.
Внимание: без кассеты ПИ/09 можно получить прямоугольный сигнал непосредственно с генератора.
2. При трех различных значениях t = R2C получите на экране осциллографа изображение импульсов зарядки и разрядки конденсатора. С помощью ручек "Вольт/делен", "синхронизация", и "время/делен" добейтесь устойчивого неподвижного изображения зарядки и разрядки конденсатора.
3. Зарисуйте координатную сетку экрана осциллографа в масштабе и кривые импульсов. Определите для всех трех значений время релаксации t (см рис 8.2, б), емкость конденсатора по известному сопротивлению и максимальное напряжение в импульсе. Вычислите постоянную времени цепи t расчетным путем и сравните ее со значением, найденным экспериментально. Найдите среднюю арифметическую ошибку измерений.
4. Не изменяя параметров схемы, подключите вход "Y" осциллографа к выходу сопротивления R1 и зарисуйте осциллограмму напряжения UR (см рис 8.2, б).
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Квазистационарные токи.
2. Дифференциальные уравнения для RC – цепи.
3. Зависимость тока зарядки и разрядки конденсатора от времени.
4. Определение t цепи из осциллограммы.
5. Расчет емкости при параллельном и последовательном соединении конденсаторов.
6. В цепи, состоящей из последовательно соединенных С = 0,3 мкФ, R = 20 кОм, Е = 12 В, определить:
а) постоянную времени,
б) максимальный заряд, приобретенный конденсатором,
в) время, через которое заряд достигнет 90% от максимального.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.