Измерение объемов тел правильной геометрической формы. Определение объема цилиндра

ИЗМЕРЕНИЕ ОБЪЕМОВ ТЕЛ ПРАВИЛЬНОЙ геометрической формы

ЦЕЛЬ РАБОТЫ: изучить устройство штангенциркуля и микрометра, на примере определения объемов тел провести обработку результатов измерений.

Объем тела можно определить несколькими способами. Если тело имеет правильную форму, то обычно измеряет его линейные размеры и по соответствующей формуле рассчитывают его объем.

Для измерения линейных размеров использует линейки, штангенциркули и микрометры.

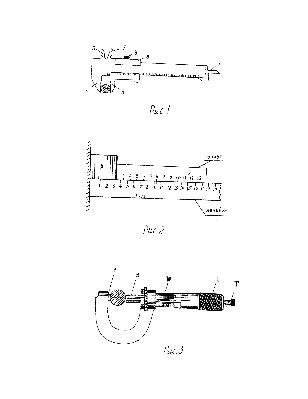
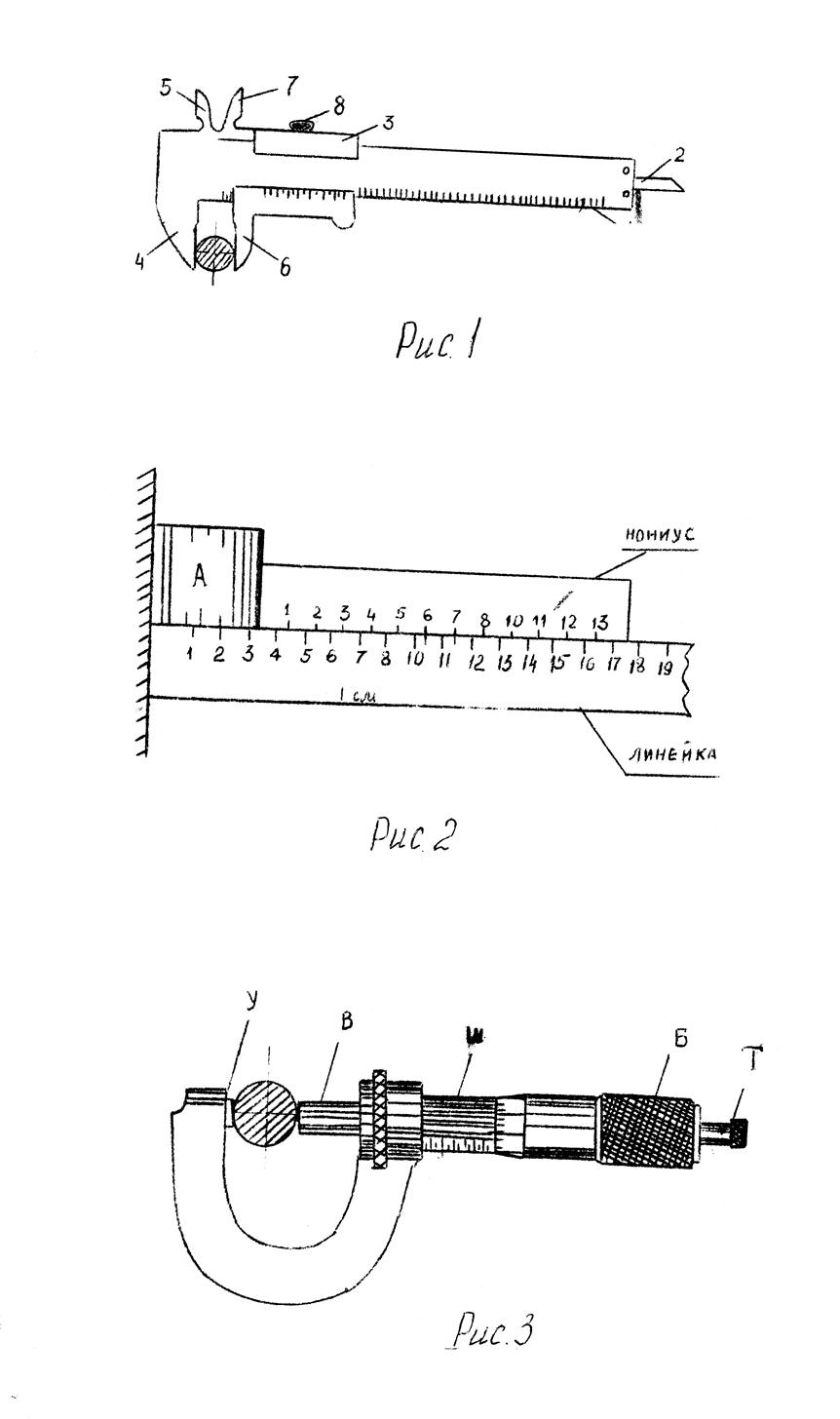
ШТАНГЕНЦИРКУЛЬ. Штангенциркуль (рис.1) представляет собой масштабную линейку I, вдоль которой может скользить скрепленная с рейкой 2 обойма 3. У линейки и обоймы имеются выступы, которые на рисунке соответственно обозначены (4-6 и 5-7). Для закрепления обоймы в нужном положении служит зажимной винт 8. В обойме имеется вырез, на нижней скошенной стороне которого нанесена шкала, называемая линейным нониусом.

Линейный нониус представляет собой небольшую линейку с делениями. Длина нониуса представляет выбирается равной длине n-1 делений шкалы масштабной линейки, т.е.

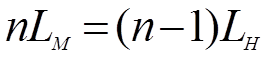 (1)

где L_H, L_M – соответственно цена деления нониуса и масштабной линейки.

Разность

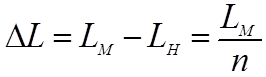 (2)

называется точностью нониуса.

Так как L_M=1 мм, то при n=10 из выражений (1) и (2) следует, что L_H=0,9 мм, длина нониуса nL_H=9,1 мм и точность =0,1 мм. Таким образом, если совместить нулевые штрихи нониуса и масштабной линейки, то последний (десятый) штрих нониуса совпадет с девятым штрихом масштабной линейки.

Рассмотрим пример измерения длины некоторого тела А (рис.2) масштабной линейкой с нониусом, точность которого равна 0,1мм. Из рисунка видно, что длина измеряемого тела больше трех и меньше четырех миллиметров; при этом седьмой штрих нониуса совпадает с десятым штрихом линейки. Следовательно, шестой штрих нониуса отступает от девятого на линейке на 0,1 мм, соответственно пятый от восьмого – на 0,7мм. Таким образом, длина предмета А равна 3,7 мм.

Если обозначить через N число целых миллиметров, а через m – номер штриха нониуса, совпадающего о каким-либо штрихом линейки, то на основе рассмотренного примера длина измеряемого тела

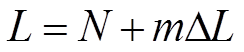 (3)

С целью облегчения отсчетов применяются также нониусы е укрепленной шкалой. Длина таких нониусов совпадает с длиной 2n-1 делений масштабной линейки, т.е.

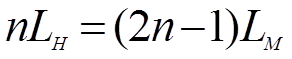
где n – число делений нониуса.

Если n=10 и L_M=0,1 мм, то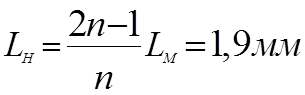

ΔL=2L_M-L_H=0,1 мм и длина нониуса nL_Н=19 мм; при пользовании таким нониусом длина измеряемого тела также определяется по формуле (2).

Существующие штангенциркули подразделяются на такие, у которых n=10 (ΔL=0,1 мм), n=20 (ΔL=0,05 мм) и n=50 (ΔL=0,02 мм).

В нерабочем положении выступы штангенциркуля 4-6 и 5-7 сдвинуты, при этом нулевой штрих нониуса совпадает с нулевым штрихом линейки. Для измерения наружных размеров измеряемый предмет размещают между выступами 4-6, которые сдвигают до соприкосновения с предметом. Для измерения внутренних размеров или расстояния между двумя точками пользуются выступами 5-7 и для измерения глубины – рейкой 2.

МИКРОМЕТР.    Измерения линейных размеров с точностью до 0,01 мм производятся микрометрами. Микрометр (рис.3) имеет вид скобы, одна сторона которой связана с неподвижной шкалой Ш. Шкала микрометра разделена на миллиметровые и полумиллиметровые деления. На концах скобы друг против друга расположены неподвижный винт упора У и микрометрический винт В, скрепленный с барабаном Б.

Шаг микрометрического винта обычно равен 1 или 0,5 мм. Пели шаг винта равен 1 мм, то барабан разделен на 100 равных частей, так что при повороте барабана на одно деление винт переместится поступательно на 0,01 мм. Если же шаг винта равен 0,5 мм, то барабан разделен на 50 равных частей, так что при его повороте на одно деление винт опять же переместится на 0,01 мм, Таким образом, точность микрометре равна 0,01 мм.

Если конец микрометрического винта привести в соприкосновение с упором, то нулевые штрихи шкалы барабана и шкалы Ш должны совпадать. Для измерений тело зажимают между упором и микрометрическим винтом и производят отсчет: целые миллиметры или полумиллиметры отсчитывают по шкале Ш до среза барабана, доли миллиметра – по шкале барабана.

Для равномерности нажатия микрометрического винта на поверхность измеряемого тела головка микрометра снабжена трещоткой Т, вращение которой вызывает перемещение винта только до его упора; после этого трещотка свободно прокручивается, издавая своеобразный треск. Поэтому при измерениях необходимо вращать не барабан Б, а трещотку Т; головку можно вращать против часовой стрелки, когда необходимо освободить тело после измерений.

Упражнение 1.    ОПРЕДЖЕЛЕНИЕ ОБЪЕМА ЦИЛИНДРА

          Объем цилиндра

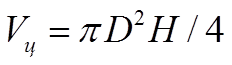 (4)

где Н – высота цилиндра; D – его диаметр.

Диаметр цилиндра измеряют микрометром, высоту – штангенциркулем.

ЗАДАНИЕ. 1. Изучить устройство микрометра и штангенциркуля. Определить цену деления основных шкал и точность прибора.

2. С помощью микрометра и штангенциркуля провести контрольные измерения диаметра D цилиндра и его высоты Н.

3. Оценить наименьшую возможную погрешность, ожидаемую ори определении объема цилиндра V_ц данными инструментами. Для оценки этой погрешности воспользоваться формулой

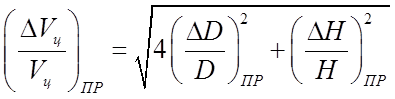 (5)

     Здесь индекс "пр." означает приборную погрешность.

4. Выполнить ряд повторных измерений величин D и H, вычислить их средние значения  и  и случайные погрешности  и . Доверительную вероятность считать равной Р=0,95.

5. По формуле (4) определить наилучше значение объема цилиндра.

6. Определить погрешность измерения объема цилиндра. Для

вычисления использовать формулу

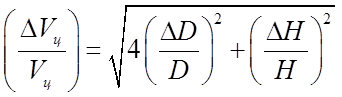 (6)

7. Оформить отчет и сделать выводи.

8. Объяснить чем отличаются формулы (5) и (б).

Упражнение 2. ОПРЕДЕЛЕНИЕ ОБЬЕМА ПАРАЛЛЕПИПЕДА.

Объем параллелепипеда

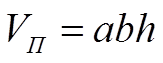 (7)

где a, b и h – соответственно длина, ширина и высота параллелепипеда.

Величины a, b и h измерить штангенщтркулем.

ЗАДАНИЕ. 1. С помощью штангенциркуля провести контрольные измерения параметров a, b и h.

2. Оценить возможную наименьшую погрешность ожидаемую при измерении объема параллелепипеда V_П. Для оценки воспользоваться формулой

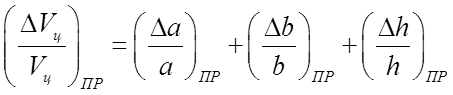 (8)

Объясните, почему при оценке аналогичной величины в упр.1 использовалось квадратичное суммирование (см. Ф-лу 5), а здесь – арифметическое?

3. Провести повторные измерения величин a, b и h в различных местах данного параллелепипеда. Вычислить их средние значения , ,  и случайные погрешности (P=0,95).

4. По формуле (7) определить наилучше значение объема.

5. Определить погрешность измерения объема параллелепипеда. Подумайте по какой формуле следует ее вычислить!

6. Оформить отчет и сделать выводы.