Атомы во внешних полях. Рентгеновские и рентгеноэлектронные спектры атомов

При этом все спектральные линии атома водорода одиночные (синглеты). Атомы щелочных металлов можно рассматривать как одноэлектронные атомы, валентный электрон которых движется в сферически симметричном, но уже не кулоновском поле. При этом снимается вырождение по орбитальному квантовому числу – энергия зависит не только от , но и от . Разрешенные правилами отбора по квантовому числу  переходы обусловливают происхождение спектральных серий щелочных металлов.

Наличие спин-орбитального взаимодействия приводит к снятию вырождения по квантовому числу , что является причиной тонкой структуры спектральных линий атомных систем. Однако в отсутствие внешних полей все направления в пространстве эквивалентны и поэтому энергии уровней не зависят от магнитного квантового числа , хотя при заданном  число , характеризующее проекцию полного момента  на ось , может принимать  значений. Кратность соответствующего вырождения равна, таким образом, . Снять это вырождение можно, создав условия, при которых некоторое направление в пространстве будет физически выделено, например, воздействием на атом внешнего магнитного или электрического поля. В соответствии с причиной, обусловившей снятие вырождения уровней, различают эффект Зеемана и эффект Штарка.

Эффектом Зеемана называется явление расщепления спектральных линий атомных систем, помещенных во внешнее магнитное поле. Так как расщепление спектральных линий обусловлено расщеплением энергетических уровней атомов, то термин «эффект Зеемана» относится также и к явлению расщепления энергетических уровней атомов, помещенных во внешнее магнитное поле.

Расщепление спектральных линий при наличии внешнего магнитного поля было впервые обнаружено в 1896 году Зееманом. Количественное объяснение этого явления с позиций классической теории дано Лоренцем. Согласно теории Лоренца при наблюдении излучения атомов перпендикулярно направлению внешнего магнитного поля спектральная линия с частотой  должна расщепляться на три компонента с частотами , , ; величина

                                           (17.1)

( - модуль напряженности внешнего магнитного поля) называется нормальным расщеплением. Компоненты расщепления обнаруживают линейную поляризацию: крайние (-компоненты) – перпендикулярную к направлению , средний (-компонент) – параллельную .

В одних случаях экспериментально наблюдаемая картина расщепления спектральных линий в точности соответствовала теории Лоренца, в других – оказалась значительно сложнее: наблюдалось число компонентов расщепления, превышающее три, а величина расщепления спектральных компонентов не описывается формулой (17.1). Последовательное описание обоих вариантов эффекта Зеемана было дано в рамках квантовой теории с учетом спинового магнитного момента атомов.

Расщепление, описываемое теорией Лоренца, было названо нормальнымили простым эффектом Зеемана. Наблюдаемая в других случаях картина расщепления называется аномальным или сложным, эффектом Зеемана. Выясним условия, при которых реализуются эти явления.

Воздействие магнитного поля приводит к изменению энергии атома , и нашей задачей теперь является определение этого изменения.

Рассмотрим аномальный эффект Зеемана. Когда атом помещен в магнитное поле, его полная энергия слагается из двух частей: из внутренней энергии атома и из энергии взаимодействия магнитного момента атома с внешним магнитным полем. Энергия взаимодействия определяется напряженностью магнитного поля , а также ориентацией и модулем магнитного момента атома. Если магнитное поле относительно невелико, так что спин-орбитальное взаимодействие в атоме сильнее, чем взаимодействие орбитального магнитного момента и спинового момента (каждого в отдельности) с внешним магнитным полем, то связь спинового и орбитального моментов атома не разрывается, то есть с магнитным полем взаимодействует полный момент атома как целое.

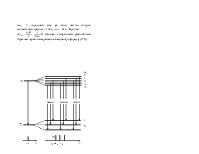
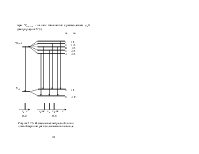
Во внешнем магнитном поле атом обладает аксиальной симметрией, поэтому в этих условиях у атома сохраняется не полный момент, а только его проекция на направление внешнего поля, то есть . Полный же момент атома прецессирует вокруг направления вектора магнитной индукции  (см. рисунок 17.1).

Дополнительная энергия атома обусловлена двумя причинами. Во-первых, атом имеет собственный магнитный момент , вследствие чего во внешнем магнитном поле с напряженностью  атом приобретает добавочную энергию

.                                        (17.2)

Во-вторых, во внешнем поле  электроны атома приобретают добавочную скорость вращения, связанную с ларморовой прецессией (атом подобен волчку; имеет место гироскопический эффект).

Мы воспользуемся первым приближением, в рамках которого дополнительной энергией, возникающей за счет прецессии, можно пренебречь. Как известно (смотри лекцию 11), оператор магнитного момента атома определяется формулой

                                        (17.3)

через магнетон Бора  и операторы орбитального () и спинового () моментов атома.

Умножив (17.3) на (-), найдем оператор взаимодействия магнитного момента атома с внешним магнитным полем .