Лабораторная работа 13
Изучение явления резонанса напряжения
низкой частоты
Цель работы: изучение явления резонанса в последовательном контуре; экспериментальное определение параметров контура.
Задание 1. Снять и построить резонансные кривые ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , соответствующие двум значениям сопротивления
цепи R и рассчитать добротность контура Q.
, соответствующие двум значениям сопротивления
цепи R и рассчитать добротность контура Q.
Задание 2. Измерить
сдвиг фаз между напряжениями на R и L, L и С,
R и С.
Приборы и принадлежности: источник переменного напряжения ЛАТР, катушка индуктивности на 2400 витков (ее R = 26 Ом, L = 0,3 Гн), батарея конденсаторов переменной емкости, реостат на 200 Ом, амперметр на 3 А, ваттметр типа Д568, вольтметры на 30, 150 и 250 В, ключ.
Теория метода
В цепи переменного тока, содержащей индуктивность L, емкость С и омическое сопротивление R, создаются условия, когда ток в цепи или резко возрастает или, наоборот, убывает. Это явление получило название электрического резонанса.
Различают резонанс токов, когда ток становится минимальным, и резонанс напряжений, когда ток достигает максимального значения. Для получения условия резонанса токов берут цепь, в которой L, С и R соединяют между собой параллельно, для получения условия резонанса напряжений берут цепь, в которой L, С и R соединяют последовательно.
В данной работе изучаются процессы, проходящие в последовательном контуре под действием внешнего переменного напряжения синусоидальной формы технической частоты (f = 50 Гц).
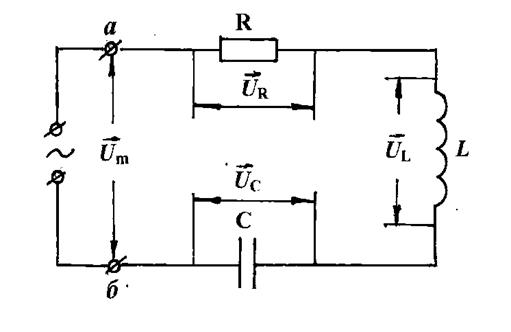
Переменное напряжение возбуждает в контуре вынужденные электромагнитные колебания (рис. 1), т. е. имеется RLС–цепочка.
|
|
Изменение емкости (или индуктивности) приводит к изменению собственной частоты контура. Когда собственная частота достаточно приблизится к частоте питающего напряжения, которое в данном случае не изменяется, в контуре возникают резонансные явления. Они проявляются в возрастании напряжений (для параллельного контура возрастают токи) на реактивных сопротивлениях по сравнению с амплитудой напряжения сети. |
Рассмотрим кратко последовательное соединение R, L, C. Ток в цепи изменяется по закону
![]() ,
(1)
,
(1)
где ![]() – амплитудное значение тока
– амплитудное значение тока
Вычислим напряжение на зажимах аб. Искомое напряжение есть сумма
![]() .
(2)
.
(2)
|
|
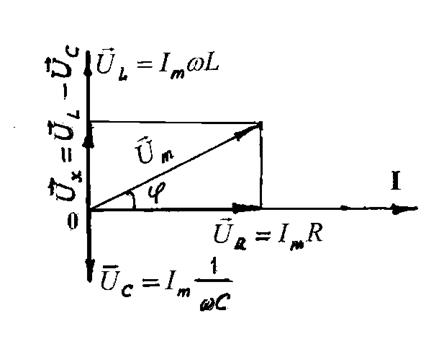
Для
сложения этих напряжений воспользуемся векторной диаграммой напряжений (рис.
2). Изменения напряжения (колебания) на R изображаются вектором, направленным вдоль оси токов и имеющим длину Изменения
же на L и C – векторами, перпендикулярными к оси токов, с длинами |
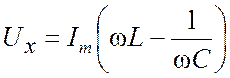 ,
,
изображаемое вектором, перпендикулярным оси токов I.
Таким
образом, полное напряжение Um можно рассматривать как сумму двух гармонических колебаний:
напряжения UR, совпадающего по фазе с током, и
напряжения Uх, отличающегося
по фазе на ![]() . UR
получило название активной составляющей напряжения, Uх – реактивной
составляющей. Оба эти колебания, складываясь, дают также гармоническое
колебание
. UR
получило название активной составляющей напряжения, Uх – реактивной
составляющей. Оба эти колебания, складываясь, дают также гармоническое
колебание
![]() ,
(3)
,
(3)
где j – сдвиг фазы результирующего напряжения. Из треугольника напряжений (рис. 2) получаем
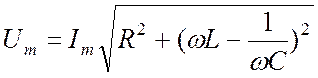 .
(4)
.
(4)
Амплитуда
тока ![]() определяется амплитудой напряжения
определяется амплитудой напряжения ![]() , параметрами R,
L, C
и частотой
, параметрами R,
L, C
и частотой ![]()
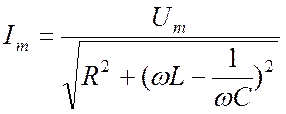 .
(5)
.
(5)
Ток
отстает по фазе от напряжения на угол ![]() ,
который зависит от параметров цепи и частоты
,
который зависит от параметров цепи и частоты
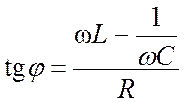 .
(6)
.
(6)
Формулу (4) называют законом Ома для цепи переменного тока. Но эта формула относится только к амплитудным, а не к мгновенным значениям напряжения тока.
Величину
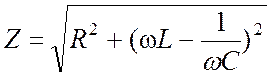 (7)
(7)
называют сопротивлением
цепи для переменного тока
(полным сопротивлением), где 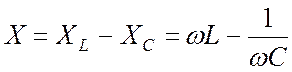 – реактивное сопротивление цепи (реактанс). Наличие реактивного
сопротивления не сопровождается выделением тепла (это – кажущееся
сопротивление).
– реактивное сопротивление цепи (реактанс). Наличие реактивного
сопротивления не сопровождается выделением тепла (это – кажущееся
сопротивление).
При
определенных значениях L и С (у нас w = const) может оказаться, что ХL = ХС
, т. е. 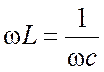 . В этом случае по формуле (6) j = 0, и изменение тока и напряжения
происходит синфазно. Амплитудное значение тока в цепи будет наибольшим:
. В этом случае по формуле (6) j = 0, и изменение тока и напряжения
происходит синфазно. Амплитудное значение тока в цепи будет наибольшим:
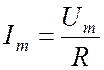 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.