Изучение явления резонанса напряжения низкой частоты (Лабораторная работа № 13), страница 2

При этом может оказаться, что U_L и U_C во много раз больше, чем U_m источника напряжения. Это явление получило название электрического резонанса напряжений. Так как U_L и U_C меняются в противофазах, то в сумме они равны нулю.

Из равенства 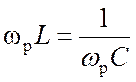 найдем резонансную частоту

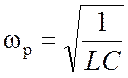.                                                       (8)

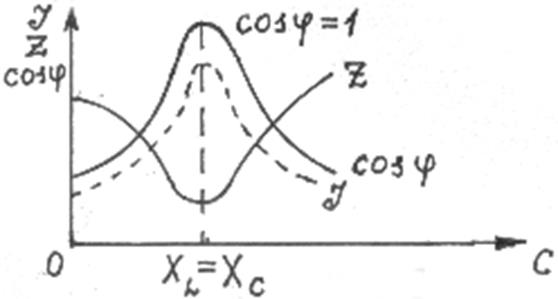
Зависимости тока , полного сопротивления Z и коэффициента мощности  цепи переменного тока в функции от емкости С (резонансные кривые) для последовательного контура приведены на рис. 3.

	Рис. 3. Резонансные кривые для последовательного контура

 

Анализ вышеприведенного материала приводит к следующим выводам:

1. При резонансе напряжений полное сопротивление цепи переменного тока принимает минимальное значение и оказывается равным ее активному сопротивлению, т. е. Z = R (так как X_L = X_C).

2. Ток в цепи достигает наибольшего значения

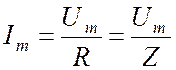.                                                        (9)

3. Коэффициент мощности принимает наибольшее значение

.

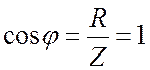4. Активная мощность  имеет максимум, равный полной мощности S, в то время как реактивная мощность равна нулю Q = Q_L - Q_C  = 0

5. U_L и U_C в зависимости от тока и I_L и I_C могут принимать большие значения, во много раз превышающие напряжение питающей цепи. При этом U_R оказывается равным напряжению питающей сети, т. е. U_R = U_m. Это явление в промышленных электротехнических установках нежелательно и опасно.

В то же время в радиотехнике и электронике широко используется резонанс напряжений (и другие резонансные явления).

Колебательный контур характеризуют его добротностью Q, которая в случае слабого затухания для последовательного контура равна

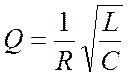.                                                      (10)

Реальную катушку можно представить как последовательно соединенные – идеальная катушка индуктивностью L и активное сопротивление R_к (резистор), равное R реальной катушки. Потери электрической энергии в конденсаторе обычно малы и не учитываются.

Описание приборов

Источник переменного тока – лабораторный автотрансформатор ЛАТР (типа ЛАТР-1: 8 А, (0…250) В или РНШ-2 – регулятор напряжения школьный: 4 А, (0…250) В).

Магазин емкостей представляет собой коробку, внутри которой смонтированы конденсаторы. Выводы одних концов конденсаторов припаяны к левой внутренней клемме, выводы вторых концов припаяны к соответствующим втулкам, расположенным последовательно на колодке крыши прибора. Центральная втулка соединяется с левой внутренней клеммой. Включение соответствующей емкости на магазине осуществляется цилиндрическим переключателем с ручкой. В цепь магазин емкостей включается с помощью клемм.

Ваттметр электродинамической системы измеряет активную мощность. Чтобы включить прибор в цепь, необходимо клеммы со звездочками замкнуть проводником. Токовая катушка (клемма 1 А) включается в цепь последовательно, катушка напряжения (клемма U) – параллельно.

Выполнение работы

Задание 1. Снять и построить резонансные кривые , , , , , соответствующие двум значениям сопротивления цепи R

1. Проверьте электрическую цепь по схеме рис. 4. Регулятор напряжения ЛАТР установите ручкой на 0.

		Рис. 4. Электрическая схема для снятия резонансных кривых

 

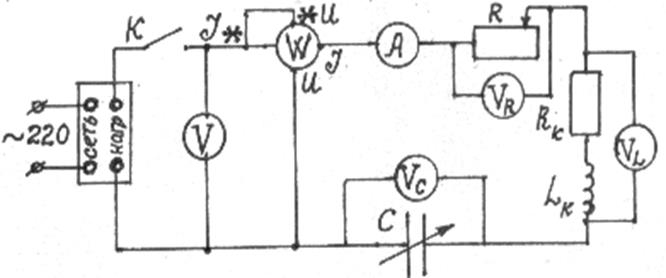2. Установите минимальную емкость батареи (0,5 мкФ), для чего ручку переключателя емкости поставьте в крайнее правое положение (или нажмите клавишу 0,5 мкФ). Введите полностью реостат R.

3. Включите ЛАТР в сеть ≈ 220 В. Замкните ключ К и с помощью ЛАТРа установите напряжение на вольтметре V не более 30 В (например, 15…30 В).

Снимите показание приборов и занесите их в табл. 1.

4. Включая последовательно все большие емкости, снимите показания приборов для каждой емкости С, пока не будет введена вся емкость батареи.

Результаты измерений занесите в табл. 1.

5. Уменьшите R цепи путем выведения половины реостата и опыт повторите снова. Результаты занесите в табл. 1

Внимание! Показания приборов умножайте на цену деления приборов.

6. Вычислите Z, Х_L, Х_C, L, Q, cosj. Из показаний приборов определите   коэффициент мощности 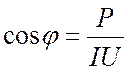 для каждого значения взятой емкости.

Таблица 1