Лабораторная работа 4
Оценка цикличности рядов посредством преобразования Фурье
Цель работы: Спектральный анализ (СА) позволяет оценить наличие циклических (сезонных) компонентов в имеющихся данных. Цель СА заключается в декомпозиции сложного временного ряда с сезонными составляющими на несколько синусоидальных функций определенной длины волны. По существу, выполнение СА над временным рядом представляет собой прохождение последнего через призму (аналогично свету) для того, чтобы идентифицировать длины волн и важность основных циклических компонентов. В результате применения СА можно определить несколько циклов различной протяженности в рассматриваемом временном ряде, который на первый взгляд представляется похожим на случайный шум.
Пакет Statistica, 6.0
1. Открыть через меню File – Open – Datasets файл данных Sunspot. Данные представляют собой наблюдаемые в период с 1749г. по 1924г. значения солнечных пятен. От этой величины зависят погодные условия на Земле, активность человека, телекоммуникации и прочие явления. В данной работе необходимо проверить цикличность солнечной активности.
2. Из меню Statistics - AdvancedLinear/NonlinearModels (Статистики – Расширенные линейные / нелинейные модели) выбрать TimeSeries/Forecasting (Временные ряды / Прогнозирование) для отображения стартовой панели TimeSeriesAnalysis (Анализ временных рядов) и открытия диалога. Отметим, что в открытом файле имеется только одна переменная Spots (Пятна), поэтому при открытии диалога эта переменная выбирается автоматически (рис.1).
Рис.1. Стартовая панель
Далее щелкнуть кнопку Spectral (Fourier) analysis для отображения диалога Fourier (Spectral) Analysis (Спектральный анализ Фурье) (рис.2).
Рис.2. Диалоговое окно спектрального анализа
Перед проведением СА построим график исходных данных. Файл данных в качестве строк содержит соответствующие годы наблюдений, поэтому для использования их на графике необходимо из опции Review series (Просмотр ряда) указать метку Casenames (Имена строк) в окне Labeldatapointswith (Метка данных точек с ..). Далее выбрать опцию ScaleXaxisinplotsmanually (Масштаб Х на графиках, вручную) и установить Min = 1 и Step (Шаг) = 10. Затем нажать кнопку Plot (График) в окне Reviewhighlightedvariable (Просмотр высвеченной переменной). График - на рис.3.
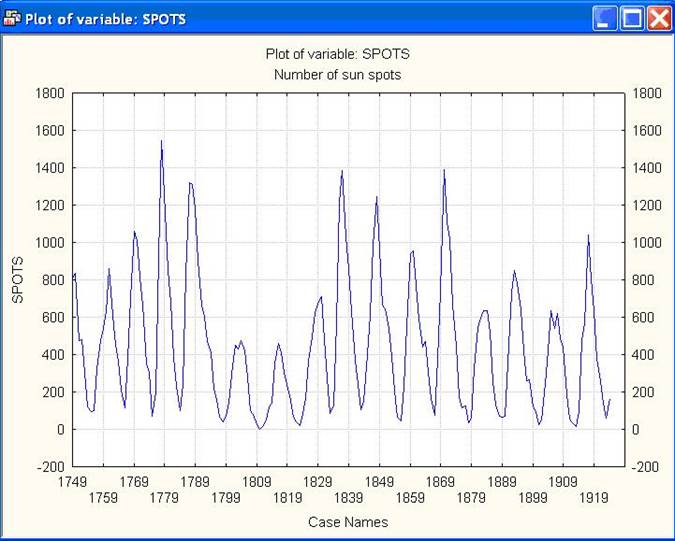
Рис.3. Исходный временной ряд
3. Полученный график имеет циклический характер и демонстрирует отсутствие тренда. Вследствие этого необходимо в окне Transformationofinputseries (Преобразование входного ряда), которое появляется при закладке Advanced (Расширенная), указать метку Detrend (Отсутствие тренда). Очевидно, что среднее значение ряда больше нуля, поэтому необходимо указать метку Subtractmean (Вычитание среднего). В противном случае на графике периодограммы может появиться большой выброс на нулевой частоте.
Теперь все готово для начала анализа. Необходимо щелкнуть ОК по кнопке SingleseriesFourieranalysis (Анализ Фурье единственного ряда), и на мониторе отобразится окно диалога SingleSeriesFourier (Spectral) AnalysisResults (Результаты спектрального анализа временного ряда).

Рис.4. Окно результатов спектрального анализа временного ряда
4. Просмотр результатов. В верхней части окна показаны некоторые суммарные статистики для этого ряда и, кроме того, 5 наибольших пиков периодограммы по частоте. Первые 3 пика имеют место при частотах: 0,0852; 0,0909 и 0,0114. Эта информация полезна при анализе очень длинных рядов (например, содержащих порядка 100000 наблюдений), которые не могут быть отображены на одном графике. Однако в этом случае может быть легко получена периодограмма, при построении которой используется вся информация. Периодограмма появляется после инициирования кнопки Periodogramпри открытой опции Quick (Быстрая) (рис.5).
5. На периодограмме наблюдаются два явных пика, наибольший из которых находится на частоте, равной примерно 0,09. Для просмотра значений всей периодограммы необходимо перейти в опцию Advanced (Расширенная) инажать кнопку Summary (Суммарный). Результаты представлены в форме таблицы (см. табл.1). Параметр Frequency (Частота) представляет собой число циклов в единицу времени (где каждое наблюдение рассматривается как занимающее единицу времени). Таким образом, частота, равная 0,0909 соответствует параметру Period (Период, т.е. количеству единиц времени, необходимых для завершения одного полного цикла), равному 11. Так как данные о солнечных пятнах представляют ежегодные наблюдения, можно сделать вывод о наличии явно выраженного 11-летнего цикла солнечной активности.
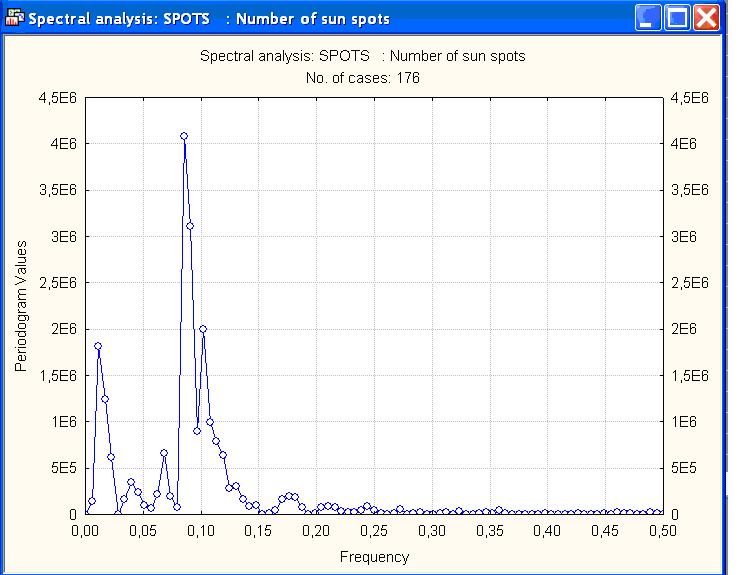
Рис.5. Периодограмма ряда
Таблица 1. Результат спектрального анализа
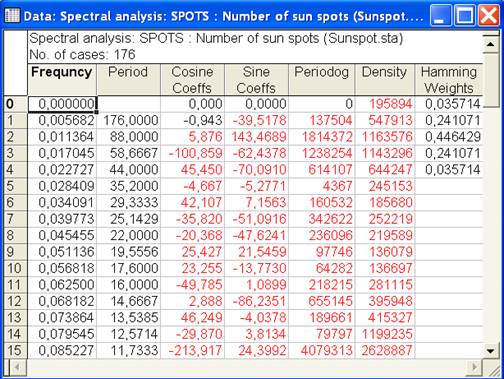
6. Спектральная плотность (СП). Обычно для получения оценок СП используется сглаживание периодограммы, при котором также происходит исключение случайных флуктуаций. Вид взвешенного скользящего среднего и ширина окна сглаживания выбирается в окне Datawindowsforspectraldensityestimates (Окна для оценок спектральной плотности), которое появляется при включении расширенной (Advanced) опции. Для рассматриваемого примера установим 5-точечное окно Хэмминга, после чего нажмем кнопку Spectraldensity (Спектральная плотность) при включенной опцииReview & plot (Просмотр и график) (рис.6).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.