Оценка цикличности рядов посредством преобразования Фурье (Лабораторная работа № 4), страница 2

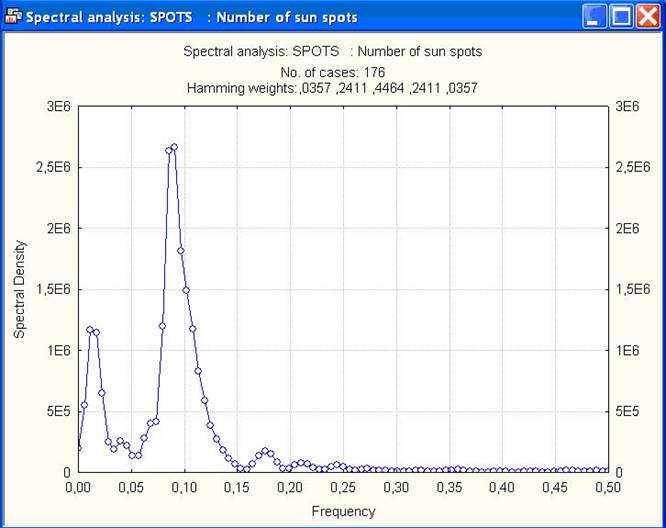
Рис.6.  Спектральная  плотность

Два  пика  теперь  видны  более  ясно. Можно  просмотреть  также  значения  периодов,  выделенных  в  этом  временном  ряду. Укажем при  включенной  опцииReview & plot   (Просмотр  и  график) метку  Period  (Период)    в  окнеPlotby   (График),  определяющем  горизонтальную  ось  графика,  и  нажмем  кнопку   Spectraldensity (Спектральная  плотность).  Появившийся  график   (рис.7) показывает  зависимость  СП  от  периода  (в  годах),  откуда  ясно  виден  четкий 11-летний  цикл  в  активности  солнечных  пятен.  Кроме  того,   имеется  еще  один  более  длинный  примерно  80- 90 - летний  цикл.

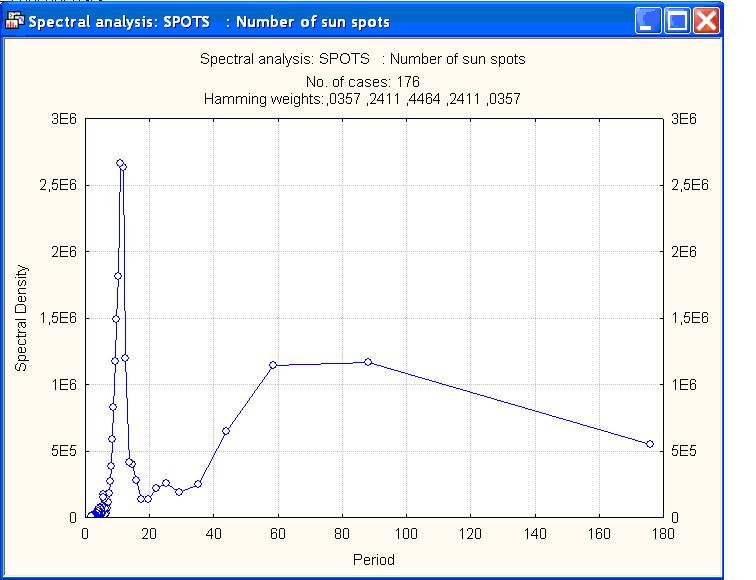
Рис.7.  Зависимость  спектральной  плотности  от  периода 

7. Частотные  окна  позволяют  найти  область  частот, которые  дают  наибольший  вклад  в  периодическое  поведение  ряда.  Это  может  быть  выполнено  путем  сглаживания  периодограммы  посредством  взвешенного  скользящего  среднего  (СС).

Положим,  что  окно  СС  имеет  ширину  m,  которая  обычно  принимается  нечетной.  Кроме  того,  между  шириной  окна  и  параметром  р,  определяющим  часть  данных,  которые  «сужают»  обрабатываемые  данные  в  начале  и  конце  ряда    за  счет  конечной  ширины,  существует  соотношение:  p = (m-1)/2.  

 Укажем  наиболее  распространенные  в  спектральном  анализе  окна:

·  Окно  Даниэля  (окно  с  равными  весами) -  этот  прием  сглаживания  сводится  к  простому  (с  равными   весами)  преобразованию  значений  периодограммы.  Каждая  оценка  СП  вычисляется  как  среднее  из  m/2 предшествующих  и  m/2   последующих   значений  периодограммы.

·  Окно  Тьюки -  здесь  веса  для  взвешенного  СС  значений  периодограммы  вычисляются  по  формуле:

   при  ,

·  Окно  Хэмминга  -  для  каждой  частоты  веса  для  взвешенного  СС  значений  периодограммы  определяются  как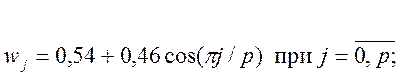 

·   Окно  Парзена  -  в  этом  случае  веса  на  каждой  частоте  определяются  следующим   образом

·  Окно  Бартлета  -  весовые  коэффициенты  здесь  рассчитываются  по  формуле

  при 

         За  исключением  окна  Даниэля  все  весовые  функции  будут присваивать  большие  значения  весов  наблюдениям,  находящимся  в  центре  окна,  и  по  мере  удаления  от центра   веса  становятся  меньше.  Во  многих  случаях  различные  окна  будут  приводить  примерно к  одинаковым  результатам,  однако  представляется  интересным   провести  анализ  одного  и того  же  ряда  с  использованием  различных  окон.

Пакет  Statgraphics,  5.1

1. Открыть  через  меню  File – Open – OpenDataFile  файл  данных  Carsales  (Продажа  машин).  Данные  представляют  собой  количество  продаваемых  машин  (в  тыс.  шт.)  по  месяцам  на  протяжении  6  лет.   

         2. Через  Special – TimeSeriesAnalysis   (Специальные – Анализ  временных  рядов)  перейти  к  опции  DescriptiveMethods (Описательные  методы).  В  появившемся  окне  выбрать  в  качестве  переменной    параметр  «sales»  (рис.8).  Остальные  поля  окна  оставить  неизменными. 

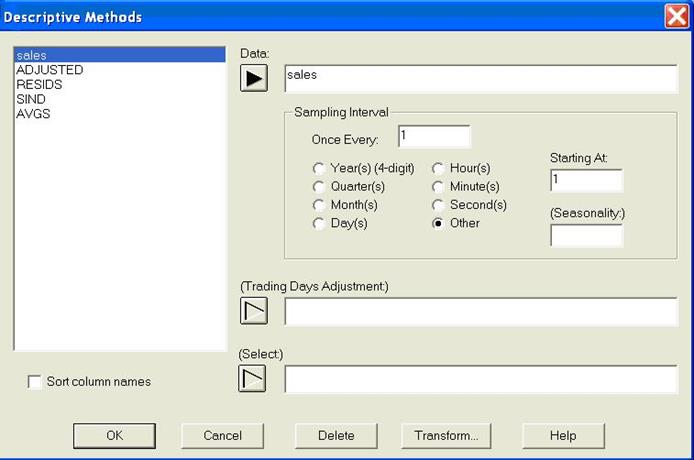
Рис.8. Входное  окно  описательных  методов

3. После  выбора  переменной  нажать  ОК,  и  на  экране  появятся результаты  вычисления.

Среди  табличных  опций,  перечень  которых  появляется  после  нажатия  желтой  клавиши  в  верхнем  ряду,  выбрать  следующие:

·  Analysis  Summary  (Итоговый  анализ);

·  Periodogram  Table  (Таблица  периодограммы).

В    табл. 2  приводятся  общие  сведения  об  анализируемом  ряде,  в  частности,  число  наблюдений,  выборочный  интервал.

Таблица 2. Сведения  об  анализируемом  ряде

 Здесь  консультант  (Advisor)  дает  следующий  совет:

 Эта  процедура  рассчитывает  различные  статистики  и  графики  для  выбранной  переменной   «sales».   Данные  перекрывают   72  временных  периода.  Выбрать  соответствующие  таблицы  и  графики  с  использованием  необходимых  опций.

В  таблице  3  приводятся  рассчитанные  значения  периодограммы 

Таблица 3. Значения  периодограммы 

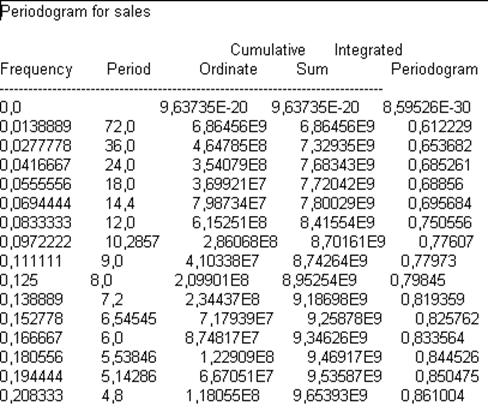
 Консультант  в  этом  случае  дает  следующий совет:

Эта  таблица  показывает  значения  ординат  периодограммы  для  переменной   «sales».  Периодограмма  строится  путем  подгонки  ряда  синусных  функций  на  каждой  из  36  частот.  Ординаты  равны  квадрату  амплитуд  этих  синусных  функций. Периодограмма  может  рассматриваться  как  анализ  дисперсии  по  частоте,  т. к. сумма  ординат  равна  общей  исправленной  сумме  квадратов  в  таблице  анализа  дисперсий.  Периодограмма  может  быть  построена путем выбора соответствующих  графических опций.  

3. Из  графических  опций,  перечень  которых  появляется  после  нажатия  третьей   клавиши  в  верхнем  ряду,  выбрать  следующие:

·  Horizontal  Time  Sequence  Plot  (Горизонтальный  временной график);

·  Periodogram  (Периодограмма).

На  рис.9 и  10   показаны,  соответственно,   исходный временной  ряд  и  периодограмма.

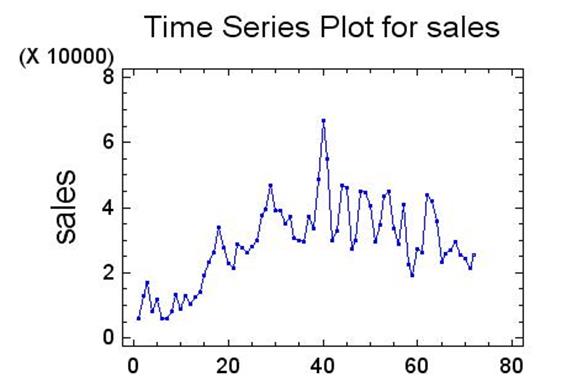
Рис.9.  Исходный  ряд

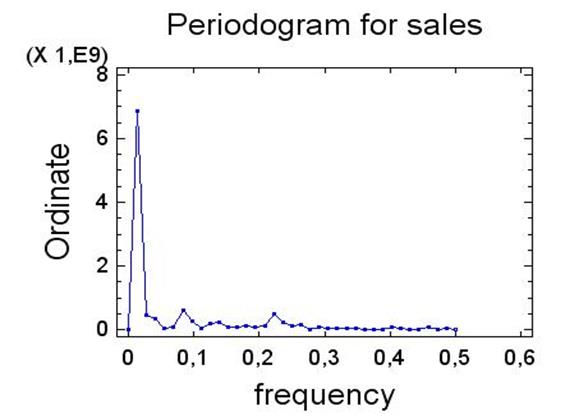
Рис.10.  Периодограмма  ряда

Анализ периодограммы  четко указывает  на  наличие  цикличности  (сезонности)  в  данном  ряде.

Задание

По пакету  Statistica, 6.0

1.Взять  файл Series_g из  имеющихся  в  пакете  данных  и  провести  спектральный  анализ  для  этой  переменной.

2. Построить  графическое  отображение  СП  в  зависимости  от  периода  при  различных   типах  окон   и  их протяженностях.

По  пакету  Statgraphics,  5.1

1. Перенести  данные  файла  Series_g в  этот пакет  и  провести  оценку  наличия  сезонных  компонентов. Определить  период  сезонности,  если  последняя  имеется.