Методы системного анализа. Задачи и области применения прогнозирования. Классификация методов прогнозирования, страница 5

Функция  является детерминированной основой прогнозируемого процесса «». С ее помощью задаются значения экзогенной переменной  для тех ситуаций, когда отсутствует воздействие случайной помехи . Функция , в свою очередь, характеризует ограничения, накладываемые на воздействие случайного процесса (помехи) . Необходимо подчеркнуть, что во многих практических задачах наряду с гипотезой о равенстве нулю математического ожидания данного случайного процесса, формулируются предположения о том, что [27]:

 почти всегда имеет постоянную дисперсию;

 обычно имеет нормальное распределение;

 очень часто некоррелированный случайный процесс.

Наибольшее распространение на практике получили модели с аддитивной (суммарно входящей) помехой следующего вида

;                                 (3.2)

Данная модель является частным случаем модели (3.1) при условии . При этом в качестве детерминированной основы прогнозируемого процесса выбирают, как уже указывалось ранее:

‑ полиномиальные функции

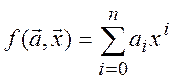;                             (3.3)

‑ экспоненциальные функции

;                               (3.4)

‑ тригонометрические функции

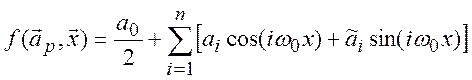,      (3.5)

где 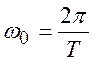,  ‑ определяется интервалом разложения функции  в тригонометрический ряд .

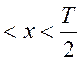
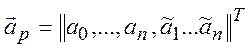Следует подчеркнуть, что на практике часто рассматривают ситуации, при которых .

После выбора класса функций, описывающих детерминированную основу прогнозируемого процесса , осуществляется поиск неизвестных параметров  на основе статистической обработки данных о конкретных значениях экзогенной переменной, полученных за период времени, предшествующий моменту времени производства прогноза (период основания прогноза, см. рисунок 3.1).

Наиболее широкое распространение на практике при статистической обработке рассматриваемых данных получил метод наименьших квадратов и различные его модификации. Напомним, что при реализации метода наименьших квадратов оценки «» неизвестных коэффициентов  находятся из условия минимума суммы квадратов отклонений искомой экстраполяционной зависимости от полученных по результатам наблюдений (измерений) значений :

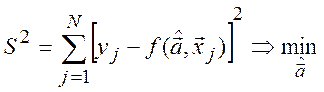.                    (3.6)

В тех случаях, когда функция  является линейной относительно неизвестных коэффициентов, а соответствующая модель прогнозирования представлена в виде:

,                   (3.7)

где  ‑ нормально распределенный случайный процесс с нулевым математическим ожиданием и априорно неизвестной дисперсией, имеется возможность аналитического решения задачи прогнозирования. После дифференцирования функции (3.6) по компонентам вектора  и приравнивания к нулю полученных результатов, формируется система алгебраических уравнений, решение которой в векторно-матричной форме имеет следующий вид [27]:

,                                  (3.8)

где  ‑ вектор-столбец независимых  наблюдений (измерений) прогнозируемого процесса ;

 ‑ матрица размерности  значений независимых переменных  (в том числе и времени ) при различных наблюдениях. Элемент , стоящий на пересечении  строки и  столбца, имеет значение, соответствующее  составляющей вектора  при  наблюдении

Статистические методы прогнозирования играют большую роль при анализе тенденций развития совершенно различных по своей природе процессов и явлений. При этом особая роль при решении задач прогнозирования отводится логистическим или, по-другому, ‑кривым, которые обобщают ранее приведенные (см. формулу (3.4)) экспоненциальные модели. Указанные логистические функции имеют следующий вид:

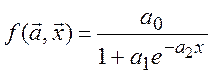,                          3.13)

где  ‑ параметры; в качестве переменной  чаще всего рассматривается время: . Используя функции вида (3.13) можно описать три наиболее характерные фазы (этапа) изменения значений прогнозируемой характеристики: этап медленного роста, этап быстрого роста, этап «насыщения» (прекращения роста), когда данная характеристика практически не изменяет свои значения (см. рисунок 3.4). Из анализа данного рисунка следует, что точка перегиба логистической кривой имеет ординату, равную , параметр ‑ характеризует скорость изменений значений переменной , которая при  равна 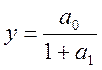, а при .

Используя логистические кривые, удалось, в свое время [15], оценить тенденции изменения скорости полета самолетов, время перехода от винтовой к реактивной авиации (см. рисунок 3.5,а), спрогнозировать тенденции изменения быстродействия ЭВМ (см. рисунок 3.5,б) при переходе от одного поколения вычислительной техники к другому поколению.