Эвристические методы прогнозирования основываются на данных и знаниях, полученных главным образом от субъекта прогнозирования. При этом данный класс методов, в свою очередь, включает в себя интуитивные (экспертные) и аналитические методы. К интуитивным (экспертным) относятся методы, основанные, прежде всего, на привлечении экспертов, являющихся специалистами в конкретной предметной области, в рамках которой осуществляется прогнозирование. Указанные специалисты определяют и оценивают тенденции и перспективы развития объектов прогнозирования, используя при этом свой личный опыт, эрудицию, догадки и эвристики.
Интуитивные методы прогнозирования получили широкое распространение на практике, так как сбор и обобщение мнений экспертов, обладающих необходимыми знаниями об объекте прогнозирования, позволяет получить довольно надежную, а в ряде случаев и единственно возможную информацию. Аналитические методы прогнозирования, основываются на логическом (теоретическом и эмпирическом) анализе содержательных (концептуальных), либо математических моделей процесса развития объекта прогнозирования, в которых задаются связи (устанавливаются отношения) между отдельными параметрами, характеризующими указанные объекты. К указанным методам, прежде всего, относятся: методы построения сценария, метод дерева целей и задач, метод коэффициентов важности, методы игрового моделирования, историко-логический метод. Данные методы прогнозирования чаще всего используются при проведении нормативного прогнозирования. Содержание перечисленных аналитических методов будет раскрыто далее в рассматриваемой главе.
Следует подчеркнуть, что при прогнозировании перспектив развития сложных организационно-технических систем целесообразно использовать комплексные (комбинированные) методы (фактографические и эвристические), которые взаимно дополняю друг друга.
В заключение данного параграфа отметим, что наряду с предложенным выше принципом классификации методов прогнозирования возможны другие подходы. Так, например, в работах все методы прогнозирования разбиваются на два больших класса:
‑ методы поискового (исследовательского) прогнозирования;
‑ методы нормативного прогнозирования.
Анализ показывает, что данный вариант классификации принципиально не отличается от предложенного ранее, так как методы поискового прогнозирования близки по своему содержанию к классу фактографических методов прогнозирования, а эвристические методы прогнозирования ‑ к классу методов нормативного прогнозирования [].
Рассмотрим более подробно содержание отдельных фактографических и эвристических методов прогнозирования, наиболее часто используемых на практике.
3.3. Статистический метод прогнозирования
Данный метод является одним из основных фактографических методов прогнозирования. Содержание рассматриваемого метода состоит в следующем. На основе анализа статистических данных о параметрах объекта прогнозирования за период времени, предшествующий моменту времени производства прогноза, устанавливается закономерность изменения и соответственно тенденция развития этих данных для периода упреждения прогноза (см. рисунок 3.1). Требуемая точность и достоверность прогноза в рассматриваемом методе существенно зависит от того, насколько правильно (оптимально в соответствии с принятыми в статистике критериями) выбран класс и конкретный вид функций, описывающих как детерминированную, так и стохастическую основу прогнозируемых процессов. При этом наиболее часто на практике используют полиномиальные, экспоненциальные, тригонометрические модели и модели, включающие в себя различные комбинации перечисленных моделей.
Пусть объект прогнозирования характеризуется некоторой совокупностью значащих переменных, которые являются наиболее существенными для описания данного объекта в соответствии с задачей прогнозирования. В этом случае можно задать математическую модель объекта прогнозирования в следующем виде:
![]() (3.1)
(3.1)
где ![]() ‑ некоторые детерминированные функции;
‑ некоторые детерминированные функции;
![]()
![]() ‑ вектор известных
параметров ОП, одним из которых является время «
‑ вектор известных
параметров ОП, одним из которых является время «![]() », в
качестве остальных параметров могут выступать различные известные величины,
влияющие на экзогенную переменную ОП – «
», в
качестве остальных параметров могут выступать различные известные величины,
влияющие на экзогенную переменную ОП – «![]() »,
», ![]() ;
; 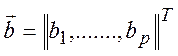 ‑ неизвестные,
подлежащие определению параметры модели;
‑ неизвестные,
подлежащие определению параметры модели; ![]() ‑
случайный процесс с нулевым математическим ожиданием.
‑
случайный процесс с нулевым математическим ожиданием.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.