В 1895 г. немецким математиком П. Гурвицем был разработан алгебраический критерий устойчивости в форме определителей, составляемых из коэффициентов характеристического уравнения замкнутой САУ:
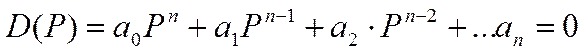
Из коэффициентов характеристического уравнения составляется определитель Гурвица
n-строк и n-столбцов по следующему правилу.
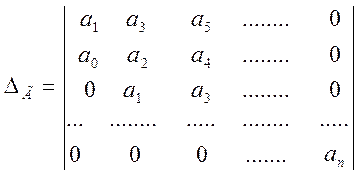
1-я строка состоит из нечетных коэффициентов
2-я строка состоит из четных коэффициентов
3-я строка, как и 1-я строка, но сдвинута на 1 элемент справа
4-я строка, как и 2-я строка, но сдвинута на 1 элемент справа и т.д.
В результате по главной диагонали определителя Гурвица располагаются все коэффициентов от a до n.
Критерий устойчивости Гурвица формулируется так:
замкнутая
САУ устойчива, если определитель Гурвица ![]() и все диагонали больше нуля:
и все диагонали больше нуля: ![]() >0. Рассмотрим пример,
>0. Рассмотрим пример,
отчеркнем в главном определителе Гурвица пунктиром диагональные миноры, тогда получим определители Гурвица.
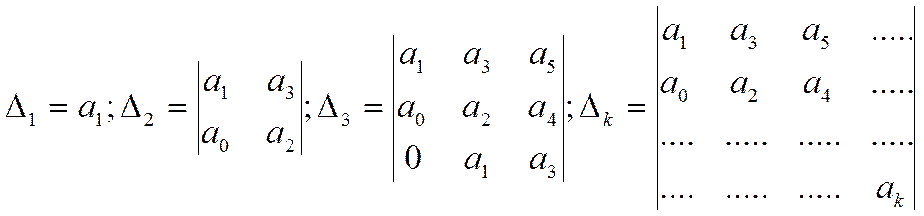
Теперь рассмотрим выполнение устойчивости по Гурвицу
1
минор: ![]() >0
>0
2
минор: ![]() >0
>0
3
минор: ![]() >0
>0
Примечание. Если Δ < 0, то система неустойчива. В этом случае нужно при заданных параметрах системы изменить какой-либо один параметр (в нашем случае это Ку), и установить его значение, при котором система будет находиться на границе устойчивости.
Воспользуемся характеристическим уравнением замкнутой САУD(P)=0:
![]()
Исходные данные:
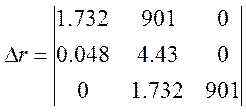
Из коэффициентов характеристического уравнения составляем определитель Гурвица:
Тогда:
1. минор:![]()
2. минор:![]()
3. минор:![]()
Вывод: Из полученных выражений следует, что все миноры получились отрицательными, и, следовательно, система неустойчивая, что и убеждается по критерию устойчивости Михайлова.
Итак, изменим исходные данные:
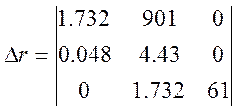
Из коэффициентов характеристического уравнения составляем определитель Гурвица:
Тогда:
1. минор:![]()
2. минор:![]()
3. минор:![]()
Вывод: Из полученных выражений следует, что все миноры получились положительными, и, следовательно, система устойчивая, что и убеждается по критерию устойчивости Михайлова.
Под параметрами системы понимают
постоянные времени, коэффициенты усиления отдельных звеньев. Некоторые из этих
параметров не подлежат изменению, другие же могут изменяться с целью
обеспечения устойчивости. Если система имеет s изменяемых параметров, то можно
говорить об s - мерном пространстве варьируемых параметров. Точки, которым
соответствует m правых и n-m левых корней характеристического уравнения n-й степени,
образуют в пространстве параметров область, обозначаемую D(m). Область
устойчивости соответственно обозначается D(0), и ее нахождение является целью
исследования. Однако отыскать область устойчивости удается, как правило, лишь
построив предварительно и все остальные D - области. Общая методика разбиения
пространства на области с различным распределением корней предложена советским
ученым Ю.И.Неймарком в 1948г. под названием D - разбиения.
В основе D - разбиения лежит нахождение уравнения и построение границы D -
разбиения, разделяющей пространства параметров на D - области. Эта граница при
большом числе изменяемых параметров s является s -мерной поверхностью, в
честном случае при s<=2 представляет собой кривую в плоскости, называемую
кривой D-разбиения. Граница D-разбиения в пространстве параметров является
отображением мнимой оси плоскости корней. Поэтому для нахождения уравнения
границы D - разбиения достаточно в характеристическом уравнении замкнутой
системы заменить р на jw. Задавая значения от до , получим все точки
пространства параметров, которым соответствует одни или несколько мнимых корней
характеристического уравнения. Штриховка кривой D- разбиения по правилу дает
выделить из всех D - областей такую область, всем точкам которой соответствует
наибольшее количество левых корней в характеристическом уравнении. Эта область
иногда называется претендентом на область устойчивости. Проверка системы на
устойчивость, выполненная для любой точки области - прендента по любому из
критериев устойчивости, позволяет ответить на вопрос, является ли
область-претендента искомой областью устойчивости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.