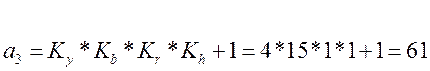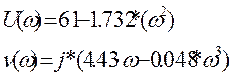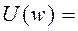 901-1.732(
901-1.732(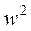 )
)
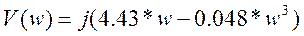
10.2.КРИТЕРИЙ
УСТОЙЧИВОСТИ МИХАЙЛОВА
Это графический критерий, удобный для
применения на практике. Он предложен в 1938 г советским ученым А.В. Михайловым и является по существу геометрической интерпретацией принципа аргумента. Пусть
дано характеристическое уравнение, которое представляет собой характеристический
полином:
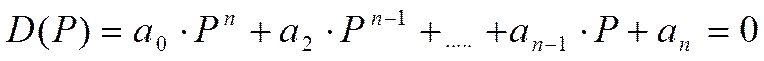
Подставим
в этот полином чисто мнимое значение P=jw, где w представляет
собой угловую частоту колебаний. При этом получим комплексную функцию:
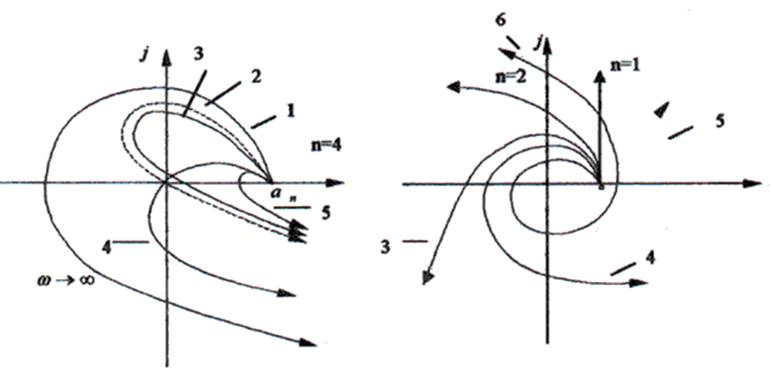
D(jw)=U(w)+jV(w),
где действительная часть
будет содержать четные степени w:
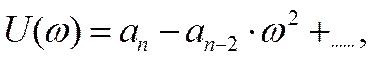
а мнимая- нечетные
степени 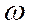
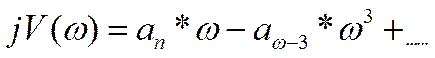
Изобразим
D(jw) в виде годографа в комплексной плоскости (кривая 1 на рис.а). Этот
годограф называется годографом Михайлова. К каждому значению w соответствуют
определенные 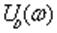 и
и 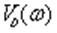 и определенная точка на
плоскости. При w=0 функция D(jw)=An, т.е. годограф начинается на действительной
оси.
и определенная точка на
плоскости. При w=0 функция D(jw)=An, т.е. годограф начинается на действительной
оси.
При 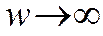 функция
функция 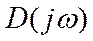 неограниченно
возрастает.
неограниченно
возрастает.
По критерию устойчивости А.В.Михайлова
Критерий Михайлова формулируется так: система устойчива, если годограф
D(jw), начинаясь на положительной действительной полуоси, огибает против
часовой стрелки начало координат, проходя последовательно n квадрантов, где n -
порядок системы.
На рис, а годограф
1 относится к устойчивой, а годографы 3,4 и 5 - к неустойчивым системам.
Условием нахождения системы на границе устойчивости является прохождение
годографа Михайлова через начало координат (штриховая кривая на рис).
Действительно, в этом случае существует значение w, при котором
D(jw)=0, т.е. характеристическое уравнение системы имеет пару сопряженных
мнимых корней p=-/+jw. Последнее и обозначает наличие в системе незатухающих
колебаний, т.е. нахождение ее на границе устойчивости. Незначительное изменение
параметров системы, в результате чего годограф D(jw) на рис. 7,а отойдет влево
или вниз от начала координат, делает систему устойчивой, а изменение параметров
в другую сторону - неустойчивой. На рис 7,б приведены годографы устойчивых
систем разных порядков до n=6.
При практическом построении годографа D(jw) прежде всего находят
точки его пересечения с координатными осями. Для этого, определив из уравнения
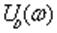
=0 значения частот,
соответствующих точкам пересечения годографа D(jw) с мнимой осью, представляют
их в выражение
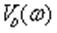
. В
результате получают соответствующие ординаты.
Аналогично находят точки пересечения D(jw) с действительной осью,
приравнивая нулю мнимую часть
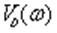
и подставляя затем найденные при этом значения w в
выражение для
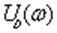
.
Собственно, после того как найдены значения w, при которых годограф
D(jw) пересекает оси координат, т.е. найдены нули
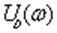
и
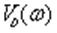
, для суждения об устойчивости системы нет
необходимости строить сам годограф. Из формулировки критерия Михайлова следует,
что устойчивость имеет место, если нули
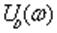
и
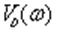
чередуются с ростом w, начиная с w=О, когда
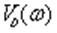
=О, а
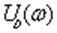
>0.
Чтобы не иметь дело с высокими степенями w, построение годографа
D(jw) можно производить по звеньям системы. Представим D(jw) таким образом:
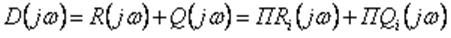
Где
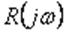
и
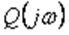
- числитель и знаменатель
амплитудно-фазовой частотной характеристики i-го звена приведенной
одноконтурной системы.
Согласно выражению (4-2), построение годографа D(jw) начинают с
построения годографов
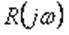
и
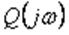
отдельных звеньев. Затем строят
годографы
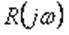
и
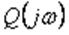
путем перемножения соответственно
годографов
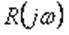
и
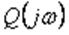
.
Годографы перемножают по обычным правилам перемножения векторов, как и при
построении частотных характеристик цепочки звеньев по характеристикам отдельных
звеньев. Для каждого значения w модули перемножают, а аргументы складывают.
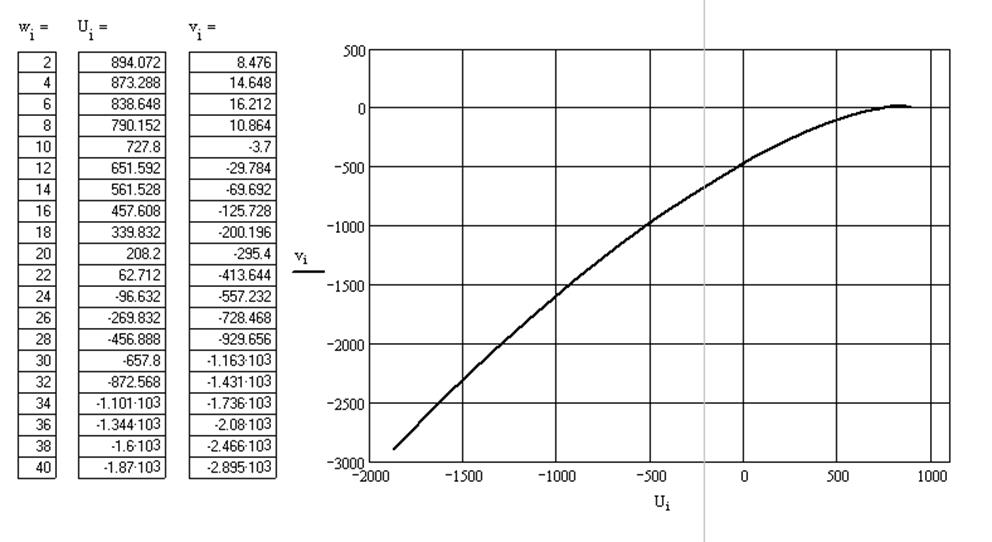
Вывод: по критерию
Михайлова САУ получилась неустойчивым.
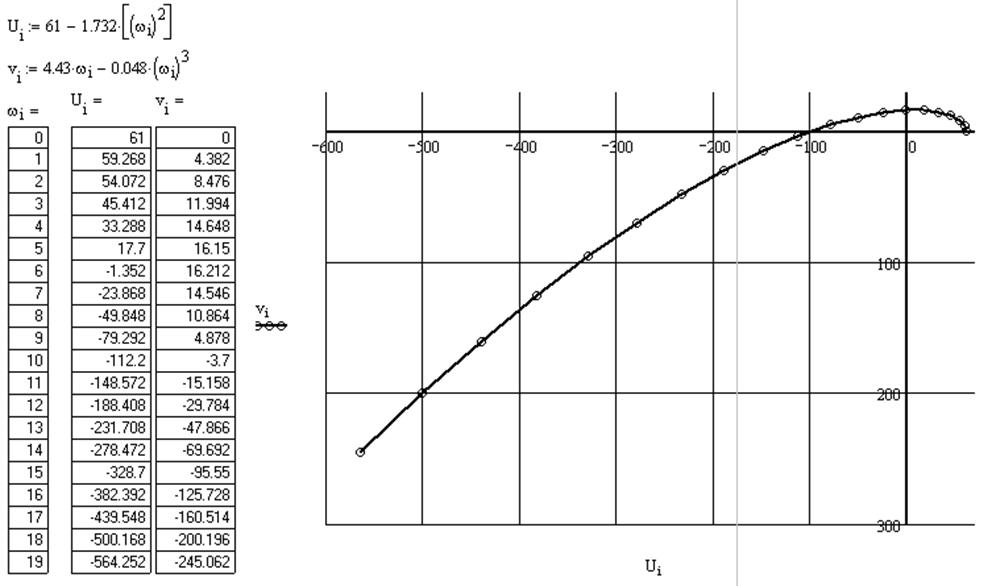
Вывод: САУ
получилась устойчивой по критерию Михайлова. Для того, чтобы САУ получилась
устойчивой, нужно уменьшитиь коэффициент усиления.Уменьшим коээфициент усиления
Ку=4 и получим 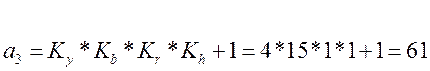
Следовательно,
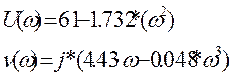
10.3.КРИТЕРИЙ
УСТОЙЧИВОСТИ РАУСА-ГУРВИЦА
![]() 901-1.732(
901-1.732(![]() )
)![]()
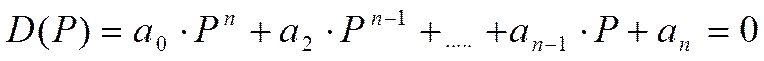
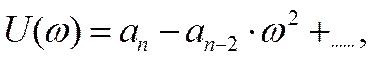
![]()
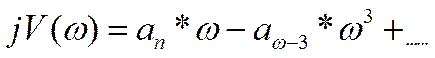
![]() и
и ![]() и определенная точка на
плоскости. При w=0 функция D(jw)=An, т.е. годограф начинается на действительной
оси.
и определенная точка на
плоскости. При w=0 функция D(jw)=An, т.е. годограф начинается на действительной
оси.![]() функция
функция ![]() неограниченно
возрастает.
неограниченно
возрастает.