10.ОЦЕНКА УСТОЙЧИВОСТИ САУ
Устойчивость – свойство системы
возвращаться в исходный или близкий к нему установившийся режим после
отклонения от него в результате любого воздействия (возмущения).
В устойчивой системе переходные процессы затухают после прекращения
действия возмущения. В неустойчивой системе переходные процессы самостоятельно
не затухают, а нарастают по величине.
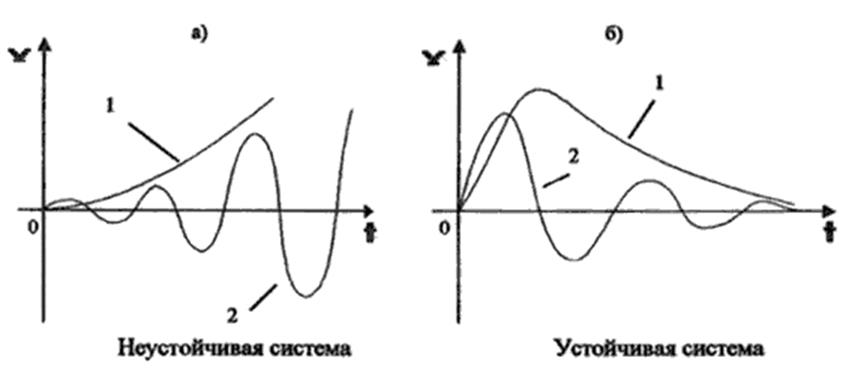
К понятию
устойчивости системы.
На рисунке
показаны типичные кривые переходных процессов в неустойчивой (рис.а) и
устойчивой (рис.б) системах. Если система неустойчива, то достаточно любого
толчка, чтобы в ней начался расходящийся процесс ухода из исходного
установившегося состояния. Этот процесс может быть апериодическим (кривая 1 на
рис.а) или колебательным (кривая 2 на рис.а).
Апериодический
расходящийся процесс может, например, возникать в САУ, если в ее управляющем
устройстве ошибочно переключить полярность воздействия на объект, в результате
чего управляющее устройство будет осуществлять не отрицательную, а
положительную обратную связь вокруг объекта. При этом управляющее устройство
будет не устранять отклонение х действовать в обратном направлении, вызывая
лавинообразное изменение.
Колебательный расходящийся процесс, как будет показано далее, может наступить,
например, при неограниченном увеличении коэффициента передачи системы,
вследствие чего управляющее устройство станет излишне энергично воздействовать
на объект, стремясь ликвидировать первоначально возникшие отклонения Х. В этом
случае при каждом очередном возврате х к нулю под действием управляющего
устройства кривая х будет пересекать ось абсцисс все с большей скоростью и
процесс в целом будет расходящимся. В случае устойчивой системы (рис.б)
переходный процесс, вызванный каким-либо воздействием, со временем затухает
апериодически (кривая 1) или (кривая 2), и система вновь возвращается в
установившееся состояние.
Таким образом, устойчивую систему можно определить также как систему,
переходные процессы, в которой являются затухающими.
Приведенное понятие устойчивости определяет устойчивость
установившегося режима системы. Однако система может работать в условиях
непрерывно изменяющихся воздействий, когда установившийся режим вообще
отсутствует. С учетом таких условий работы можно дать следующее, более общее
определение устойчивости: система устойчива, если ее выходная величина остается
ограниченной в условиях действия на систему ограниченных по величине
возмущений.
Рассмотрим, от чего зависит устойчивость системы, чем она
определяется.
Обратимся для этого к уравнению динамики системы где:
х=Wз(p)f
Где
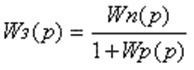
Любую передаточную функцию можно
представить в виде правильной дроби.
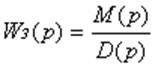 ;
; 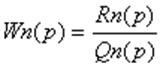
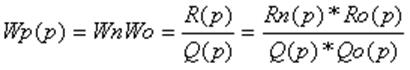
Освободившись от дробей в
числителе и знаменателе передаточной функции, можно представить ее так:
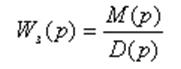
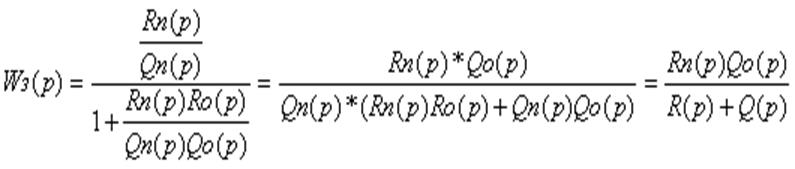
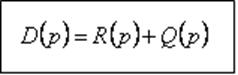 - сумма числителя и знаменателя передаточной
функции разомкнутой системы.
- сумма числителя и знаменателя передаточной
функции разомкнутой системы.
И
соответственно перейти к обычной форме записи в виде дифференциального
уравнения
y(t)=W(P)f(t)
y(t)-регулируемая ( выходная величина );
f(t)-возмущающая величина;
W(P)- передаточная функция САУ в
операторной форме.
Передаточную
функцию W ( P ) всегда можно записать в виде правильной дроби:
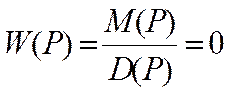
Тогда ДУ приобретает вид:
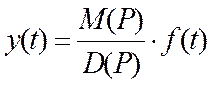 или
или 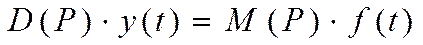
- это неоднородное ДУ. Для изменения
переходных процессоров исключим возмущающее воздействие f(t)=0. Тогда получим
однородное ДУ:
D(P)=
y(P)= 0-это уравнение
описывает собственные колебания системы.
Полином
D(P) степени n от оператора 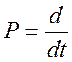 характеризует
свободное движение регулируемого объекта с регулятором. Он называется ХАРАКТЕРИСТИЧЕСКИМ
ПОЛИНОМОМ и может быть представлен в виде:
характеризует
свободное движение регулируемого объекта с регулятором. Он называется ХАРАКТЕРИСТИЧЕСКИМ
ПОЛИНОМОМ и может быть представлен в виде:
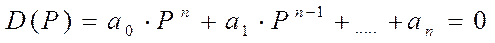 ,
,
где
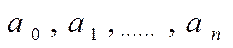 - постоянные коэффициенты
- постоянные коэффициенты
n- порядок характеристического
уравнения.
10.1
Характеристическое уравнение системы

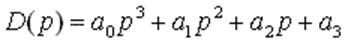
Характеристический полином замкнутой САУ:
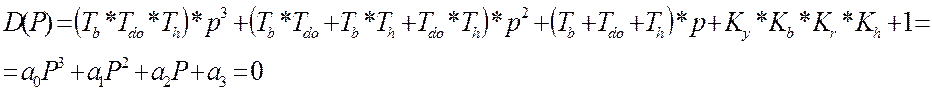
Для заданной системы:
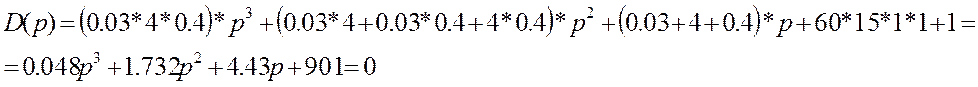
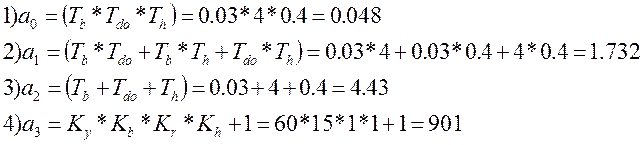
Комплексный
полином
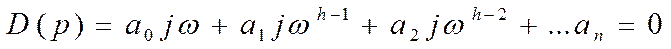
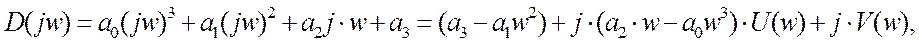
где
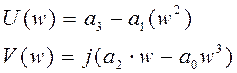

Таким образом, получим следующее выражение:

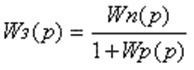
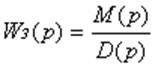 ;
; 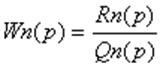
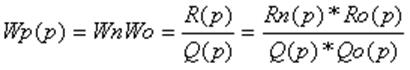
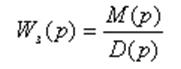
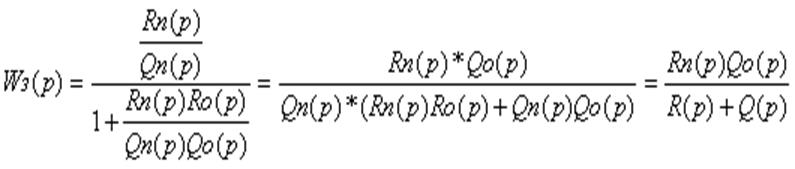
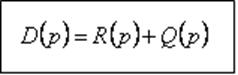 - сумма числителя и знаменателя передаточной
функции разомкнутой системы.
- сумма числителя и знаменателя передаточной
функции разомкнутой системы.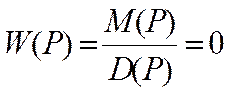
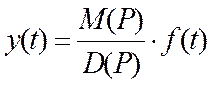 или
или ![]()
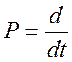 характеризует
свободное движение регулируемого объекта с регулятором. Он называется ХАРАКТЕРИСТИЧЕСКИМ
ПОЛИНОМОМ и может быть представлен в виде:
характеризует
свободное движение регулируемого объекта с регулятором. Он называется ХАРАКТЕРИСТИЧЕСКИМ
ПОЛИНОМОМ и может быть представлен в виде:![]() ,
,![]() - постоянные коэффициенты
- постоянные коэффициенты
![]()
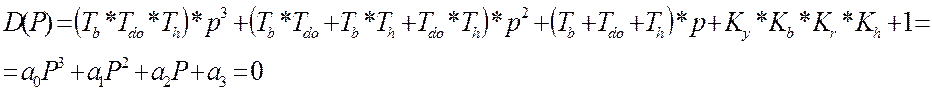
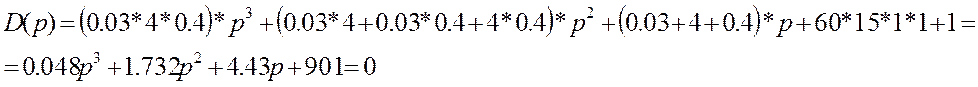
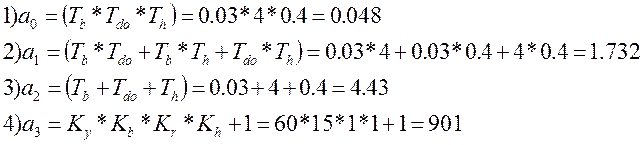
![]()
![]()
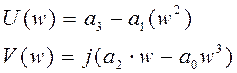
![]()