Поэтому, чем меньше количество относительно больших лепестков Gdet(q), тем ниже МО УМБЛ. Для ДН КБ таких лепестков два (по одному с каждой стороны от ГЛ), для ДН, соответствующего шестиступенчатому ВО, таких БЛ двенадцать, а для ДЧ ДН все БЛ исходной ДН одинаковые, поэтому в искаженной ДН модуль координаты наибольшего БЛ оказывается практически любым на отрезке qÎ[qГЛ, 1].
При возрастании дисперсии ПН помех МО и дисперсия УМБЛ ДН для шестиступенчатого ВО и ВО КБ становятся мало отличающимися, а для ДН ДЧ математическое ожидание УМБЛ по-прежнему выше.
Значения mk и s2k для искаженных ДН, соответствующих шестиступенчатому ВО и окну КБ, мало отличаются. Таким образом, при ОИП, особенно ПН, основные параметры искаженных ДН для ступенчатых ВО не менее устойчивы и не уступают, а по ШГЛ даже превосходят ДН для ВО КБ.
ДН ДЧ обладают меньшей устойчивостью УМБЛ к воздействию помех и искажений, а mk и s2k для них всегда существенно больше. Единственное достоинство, которое сохраняется, - это наименьшее МО ШГЛ.
В таблице приведены данные и для 4-ступенчатого ВО, обеспечивающего более высокий исходный УМБЛ ДН (-28,8дБ), чем другие ДН при отсутствии искажений и помех. Несмотря на это, в случае s2n=0,1, т.е. при ОИП, МО и дисперсия УМБЛ, а также mk и s2k для возмущенных ДН, соответствующих 4-ступенчатому ВО, практически такие же, как и для двух других рассматриваемых ВО. Однако, четырехступенчатое ВО при этом обеспечивает наименьшее МО ШГЛ.
Отсюда следует, что при определенных условиях не имеет смысла использовать более высокоорганизованные ВО. При равных s2n, s2DA и s2Dj ПК искажения приводят обычно к большему МО и дисперсии УМБЛ, а также дисперсии ШГЛ, чем ПН помехи. С другой стороны, ПН помехи сильнее влияют на рост mk и s2k.
Методика выбора АФ для АР с заданным NА
Предположим, что требуется обеспечить МО УМБЛ не хуже Yтр и ШГЛ не больше dqтр при максимальном уровне помех и искажений, характеризуемых параметрами s2n, s2DA, s2Dj и диапазоном значений gdÎ[gmin, gmax].
Первый шаг - проверить, а могут ли требования по ШГЛ и УМБЛ быть удовлетворены в детерминированной постановке. Для этого берем ВО ДЧ, задаем Yтр и определяем для него dqДЧ0.5. Если выполняется соотношение dq ДЧ0.5£0,8dqтр, то, возможно, задача имеет решение в статистической постановке для других ВО, кроме ВО ДЧ. Если же условие не выполняется, то следует выбирать ДЧ распределение с dqДЧ0.5»(0,96¼0,98)dqтр.
Тогда, с одной стороны, остается небольшой запас по ШГЛ, который необходим в связи с эффектом небольшого увеличения ШГЛ ДН при воздействии помех и искажений по сравнению со случаем их отсутствия, а, с другой стороны, УМБЛ неискаженной ДН ДЧ оказывается ниже требуемого и, следовательно, имеется запас на его рост вследствие влияния помех и искажений.
При выполнении условия dqДЧ0.5£0,8dqтр в первую очередь следует провести статистический анализ возмущенных ДН для ВО, обеспечивающих исходный ШГЛ ДН, не хуже 0,98dqтр и исходный УМБЛ, на 3¼6дБ ниже требуемого.
При этом целесообразно проанализировать статистические характеристики ДН, соответствующих ступенчатым АФ, АФ КБ, а также других АФ, для которых ШГЛ в наименьшей степени отличается от ШГЛ ДН ДЧ (по результатам детерминированного анализа), а устойчивость основных параметров искаженных ДН к дестабилизирующему влиянию помех и искажений высокая.
Если при заданных максимальных s2n, s2DA, s2Dj и gd требования к УМБЛ удовлетворить не удается, то надо либо ужесточить требования к уровню помех и искажений, либо сделать менее жесткими требования к характеристикам возмущенных ДН - увеличить допустимый УМБЛ и провести описанную выше последовательность действий снова.
Разработанный комплекс программно-алгоритмических средств позволяет реализовать все перечисленные выше этапы проектирования, в частности рассчитать МО и дисперсию основных параметров искаженных ДН.
Предоставленные сервисные возможности гистограммного анализа распределений параметров искаженных ДН позволяют оценить закон распределения, а также определить границы изменения случайных значений (минимум и максимум), вероятность выхода значений ШГЛ и УМБЛ за установленные пределы.
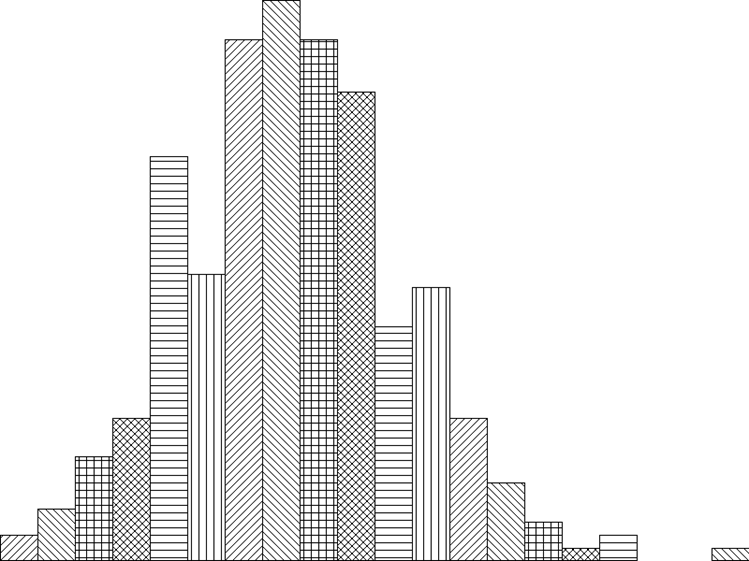
Гистограмма распределения значений УМБЛ
(минимум - 0,0267, максимум - 0,0389)
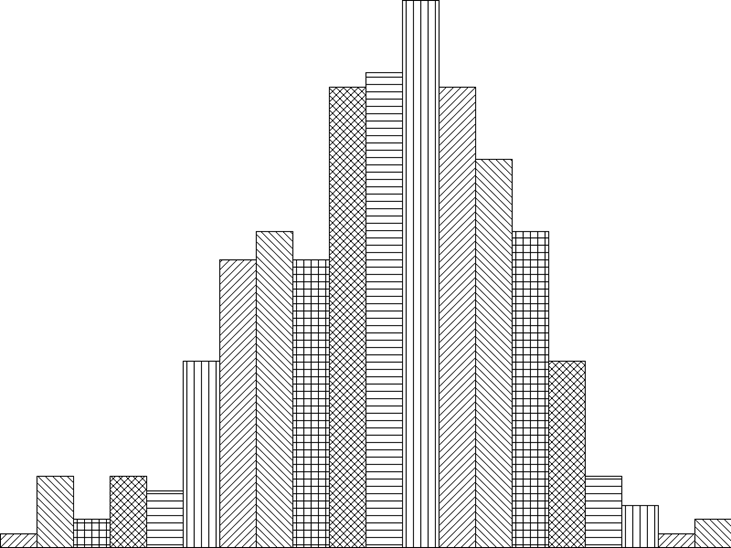
Гистограмма распределения значений ШГЛ
(минимум - 0,01205, максимум - 0,01223)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.