Антенны спутниковых систем связи: основные характеристики и требования к ним, методы обеспечения. Одномерные антенные решетки, страница 2

Пуассона (с варьируемым параметром  a_П);

Хэннинга-Пуассона (с варьируемым параметром  a_ХП):

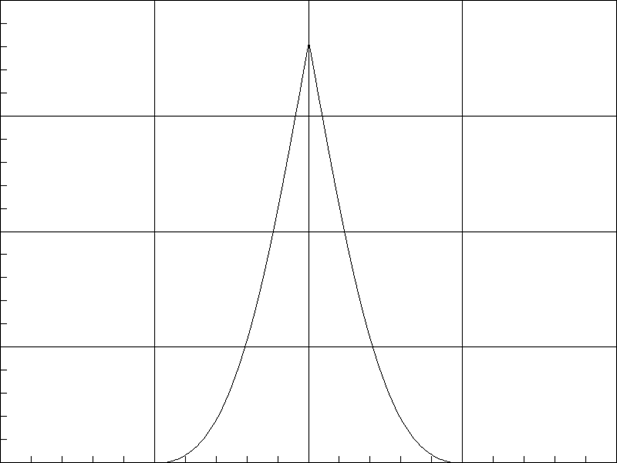
ВО Хеннинга-Пуассона при a_ХП=2

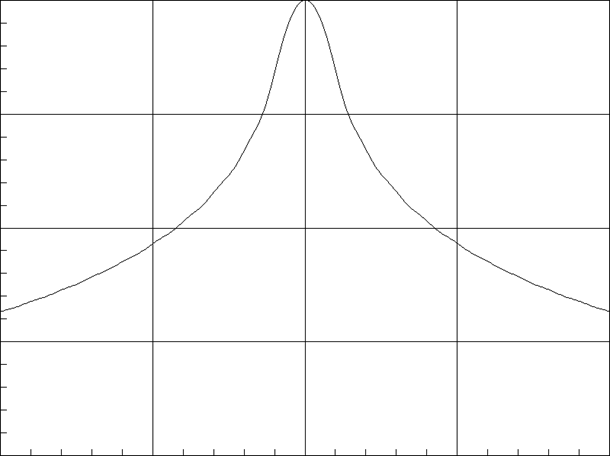
 ДН для ВО Хеннинга-Пуассона при a_ХП=2

Другие виды амплитудно-фазовых распределений

Абеля-Коши-Пуассона (с варьируемым параметром  a_АКП);

Треугольное (Бартлетта):

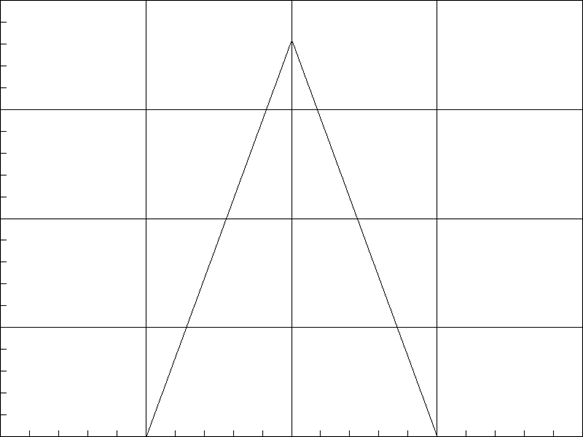
ВО Бартлетта

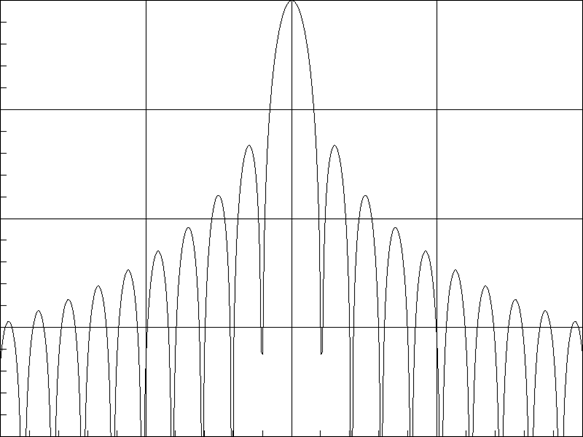
ДН для ВО Бартлетта

АФ Бомана, АФ Риса, АФ Хэрриса-Блэкмана-Наттола и т.д.

Сканирование ДН осуществляется за счет введения линейного фазового множителя или использования межэлементных диний задержки.

ВО суммарно-разностного типа

К суммарно-разностным ВО принадлежат окна Ханна, Хэмминга и Блэкмана-Наттола и др. 

Полагается, что парциальные ВО w_ko(x), входящие в сумму

,  

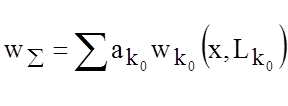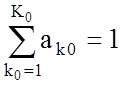
могут быть идентичного типа, например, cos[(px/L_x)^k1 (где k1 - целое число), но при этом w_ko(x) могут быть определенными (не равными нулю) на неодинаковых интервалах xÎ[-L_ko/2 ;L_ko/2], L_ko£L_x.

Таким образом, появляется дополнительная степень свободы для решения оптимизационных задач, связанная с возможностью варьировать не только амплитудные коэффициенты a_ko, число компонент K и тип парциальных ВО w_ko(x, L_ko), но и параметры {L_ko}, вернее, соотношения {L_ko/L_x}.

Это позволяет решать ряд важных задач. Например,  используя в качестве одного из компонент ВО Дирихле с L₁=L_x при a_ko>0, ₀ можно удовлетворить конструктивно-технологическое требование w_Smin>a_min за счет выбора a₁.

Таким путем были синтезированы и ВО ступенчатого вида, показанные ранее.  

Полагая, что некоторые a_ko могут быть отрицательными при выполнении  условия 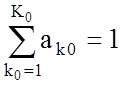 удается синтезировать ряд интересных ВО: например, ВО Бартлетта с плоской вершиной как результат вычитания треугольника с L₂/L=0,16 из треугольника L₁/L_x=1.

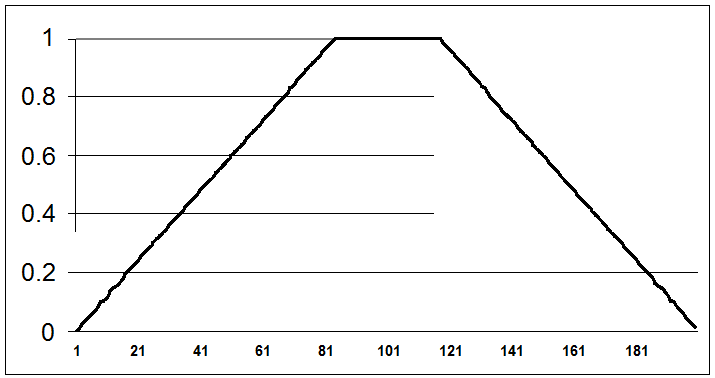n

ВО Бартлетта с плоской вершиной (N_A=200)

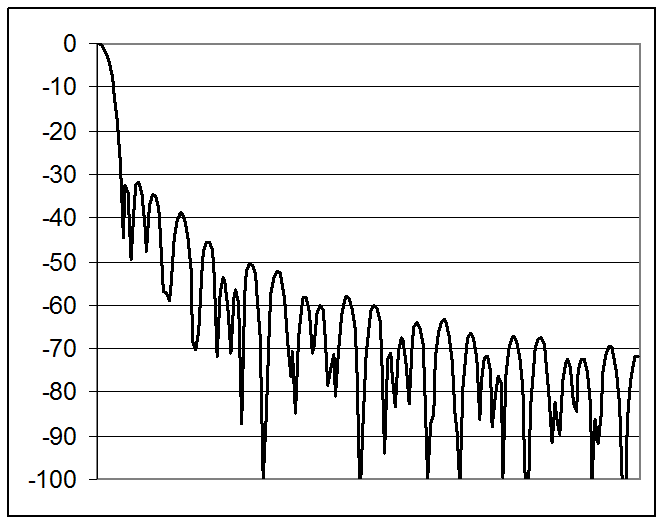q

ДН G(q), дБ, для ВО Бартлетта с плоской вершиной

Для такого ВО по сравнению с оригиналом УМБЛ ДН снижается на 5 дБ и при этом на 3% сужается ГЛ.

Проектирование одномерных АР

(выбор АФ среди возможных вариантов)

1.  Определить, существуют ли АФ, для которых параметры соответствующих ДН удовлетворяют требованиям и ограничениям ТЗ, среди оптимальных АФ Дольфа-Чебышева (ДЧ) и Кайзера-Бесселя (КБ) при максимально возможном (допустимом) числе элементов антенной решетки.

2.  Если такие АФ существуют, то определить диапазон числа элементов антенной решетки, при которых требования ТЗ можно удовлетворить (найти граничные значения).

3.  Проанализировать характеристики ДН для АФ, для которых известно, что характеристики их ДН не слишком сильно отличаются от характеристик ДН ДЧ и КБ.

4.  Определить диапазон изменения параметров АФ и АР, при которых можно удовлетворить требования ТЗ.

5.  Принять решение об использовании той или иной АФ с учетом основных характеристик соответствующих ДН, а также других аспектов (например, простоты реализации АФ в АР рассматриваемого класса).

Основные закономерности: увеличение числа элементов АР для фиксированного типа АФ приводит к сужению ГЛ, сохранению УМБЛ ДН и небольшому возрастанию k. Снижение УМБЛ, как правило, приводит и к уменьшению k. Снижение УМБЛ достигается за счет увеличения ШГЛ ДН. Увеличение ССБЛ сопровождается возрастанием ШГЛ и уменьшением k.        

ДН антенных решеток при наличии

помех и искажений (возмущений)

На практике улучшению характеристик БЛ ДН неизбежно препятствуют помехи и искажения АФР, обусловленные разнообразными факторами, включая следующие:

–  внешние пространственно-некоррелированные аддитивные помехи;

–  аддитивные помехи внутреннего (аппаратурного) происхождения, которые также можно полагать независимыми для различных каналов;

–  неидентичность АЧХ и ФЧХ каналов, взаимовлияние элементов МАР;

–  турбулентность среды распространения колебаний, приводящая к флуктуациям амплитуды и фазы фронта волны, характеризуемых заметной степенью пространственной коррелированности;