Физические основы радиоэлектроники. Электрические цепи. Законы Кирхгофа. Элементы цепи. Идеальные элементы цепей при гармоническом воздействии, страница 5

Мы должны учесть следующее. Запас энергии в любом реальном накопителе не может измениться скачком, мгновенно. Это требует источника бесконечной мощности. Следовательно, напряжение на конденсаторе меняется непрерывно и . Таким образом, если входное напряжение изменилось скачком и стало, то всё это напряжение в первый момент падает на сопротивлении . Значит , а . Это и есть начальные условия для тока. В итоге, .

Часто советуют составлять и решать дифференциальное уравнение для той величины, которая меняется непрерывно. В данном случае для напряжения , хотя уравнение и неоднородное. Решение уравнения имеет такой вид. . Здесь  есть частное решение неоднородного уравнения. Постоянная  находится с помощью начального условия . В результате, напряжение  меняется непрерывно, а ток меняется скачком при , как на рис. 1.10.

В цепях с индуктивностью запасённая энергия определяется током, поэтому непрерывно должен меняться ток. Однако в трансформаторе токи в обмотках могут меняться скачком одновременно, поскольку запас энергии определяется суммарным магнитным потоком обмоток.

2). Подключение гармонического сигнала  (или ).
Напишем сразу общее решение уравнения для напряжения.

  (или ); .

Первое слагаемое есть решение однородного уравнения. Оно описывает переходной затухающий процесс, связанный с включением источника сигнала в момент . Мы можем считать , поскольку включение гармонического сигнала произошло очень давно, и переходной процесс уже закончился.

Второе слагаемое есть частное решение неоднородного уравнения. Оно определяет вынужденный процесс. Для гармонического сигнала (бесконечного во времени) нас интересует только это решение. Для линейной цепи в качестве решения мы получим гармонический сигнал той же частоты. Надо определить только амплитуду и фазу. К этому сводится всё решение.

Вспомним, как получается решение неоднородного уравнения. Ищем решение в виде: . Подставляем это в уравнение и приравниваем коэффициенты при функциях sin и cos. Имеем: ; . После преобразований получим написанное выше решение.

1.9.  Символический (операторный) метод решения.

Он представляет собой другой, более простой способ получения решения уравнения для гармонического сигнала. Рассмотрим снова цепь последнего примера и соответствующее уравнение.  . Полагаем теперь . Тогда . Надо определить только . Дифференцирование такого сигнала сводится просто к умножению на  (потому и упрощение). Для определения  получается уже алгебраическое уравнение  .  Откуда комплексная амплитуда  . В итоге: 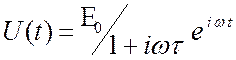. Если взять мнимую часть этого выражения, то мы сразу получим результат примера 1.8.4.2.

Это и называют символическим (или операторным) методом решения. Слово «символический» подчёркивает нереальность таких комплексных сигналов (символов). Однако с ними часто проще, удобнее работать. Все токи, напряжения, сопротивления теперь стали комплексными. Комплексное сопротивление , где  есть активная составляющая, а  - реактивная, называют импедансом. Комплексному числу мы сопоставляем вектор на плоскости. Поэтому говорят о векторах тока, напряжения, сопротивления. Рисуют векторные диаграммы. Это очень удобно, наглядно. К этому надо привыкнуть.

1.10.  Идеальные элементы цепей при гармоническом воздействии.

Будем считать параметры элементов , и  постоянными.

а). Активный элемент.  Пусть .  Тогда  . Напряжение и ток синфазны. Мгновенная мощность . Средняя за период мощность , где  есть эффективное значение тока (корень из среднеквадратичного значения). Электрическая энергия переходит в тепловую.

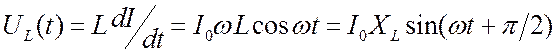б). Идеальный индуктивный элемент. Пусть опять  . Тогда . Напряжение опережает ток на четверть периода (сдвиг по фазе на ). Ситуация изображена на рис. 1.11а.  есть индуктивное сопротивление, равное отношению амплитудных значений напряжения и тока (отношение  не даёт сопротивления, поскольку оно зависит от времени). Мгновенная мощность . Средняя мощность равна нулю. Выделения энергии нет, есть обмен. Энергия дважды за период запасается в индуктивном элементе и отдаётся обратно в цепь. Поэтому говорят, что сопротивление  реактивно.