Физические основы радиоэлектроники. Электрические цепи. Законы Кирхгофа. Элементы цепи. Идеальные элементы цепей при гармоническом воздействии, страница 2

Типичная задача теории цепей такова. Конфигурация цепи (провода), источники и другие элементы считаются заданными. Искомыми величинами в цепи являются токи и напряжения. Находятся они из законов Кирхгофа для мгновенных значений токов и напряжений.

Первый закон. Алгебраическая сумма токов в узле равна нулю (заряд в узле накапливаться не может). Подтекающий к узлу ток считается положительным, оттекающий - отрицательным.

Второй закон. Для любого контура сумма падений напряжения на его элементах равна сумме ЭДС (суммарная работа при перемещении электрического заряда по замкнутому контуру равна нулю).

Число уравнений должно соответствовать числу независимых переменных (токов и напряжений).

1.4.  Элементы цепи.

Элементы цепи обычно идеализируют. В частности, их считают сосредоточенными, четко локализованными. Это накладывает ограничения на их величины. Например, емкость двух изолированных близко расположенных проводников длиной в несколько см. составляет единицы пф и четко локализовать ее (сосредоточить) иногда невозможно. Если в цепи есть конденсаторы, емкость которых много больше взаимной емкости проводов, то последнюю просто не учитывают. Аналогичная ситуация возникает с малыми индуктивностями порядка 1 мкГн. Таким образом, большие значения R, L и C мы можем считать сосредоточенными, а маленькие, далеко не всегда. В соответствии с таким делением элементов, цепи тоже делят на цепи с сосредоточенными элементами и цепи с распределёнными элементами.

Элементы цепи делят на активные и пассивные. К активным относят источники тока или напряжения, поставляющие энергию в цепь, или генераторы, создающие сигнал. К пассивным относят элементы, потребляющие энергию, обычные сопротивления R, или запасающие ее, индуктивности L и емкости C.

Для пассивных идеальных элементов мгновенные значения тока и напряжения связаны следующими соотношениями.

Сопротивление R.    или  .

Индуктивность L. 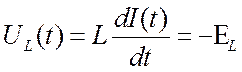 . При составлении уравнений удобнее иметь дело не с ЭДС E_L, а с падением напряжения на индуктивном элементе. Иногда используется и более общее соотношение 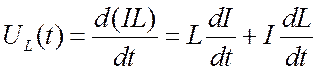, когда индуктивность зависит от времени.

Емкость C. 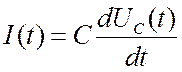  или 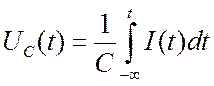. Более общее соотношени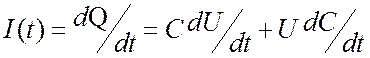е: , где  есть заряд.

Еще не надо забывать элемент взаимной индукции, рис. 1.3.  При наличии связи между катушками, ЭДС индукции в каждом контуре может возникать как при изменении тока в этом же контуре, так и при изменении тока в другом. Обычно пишут:  есть взаимная индуктивность;  - коэффициент связи.  Дополнительное падение напряжения в каждом контуре  за счет связи записывают так: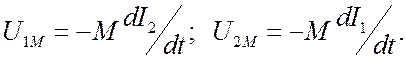

При последовательном соединении элементов складываются напряжения, ток единый. При параллельном соединении складываются токи в узле, напряжение общее.

Реальный элемент мы всегда можем изобразить комбинацией этих идеальных элементов. Например, конденсатор. Простейший вариант, идеальный конденсатор изображён на рис. 1.4а;  более сложный вариант, реальный конденсатор с утечкой – рис. 1.4б; еще сложнее, с учетом индуктивности выводов – рис. 1.4в.

Обратимся к активным элементам, источникам. Их делят на независимые и зависимые. Для первых считается заданной ЭДС, которая не зависит от тока, от отбираемой мощности. Это типичная идеализация. Напряжение на зажимах реального источника зависит от тока, от величины нагрузки. Это частично учитывается за счет внутреннего сопротивления источника, но не полностью.

Зависимыми называют управляемые источники (лампы, транзисторы). Они воспроизводят подводимый сигнал, изменяя величину напряжения или тока. Например, пусть ЭДС зависимого источника пропорциональна входному току. Тогда пишут . Для зависимых источников ЭДС равна нулю, если управляющего сигнала нет.

Любой источник мы можем изобразить как источник напряжения или как источник тока, рис. 1.5. Эквивалентность цепей реализуется, если .