Физические основы радиоэлектроники. Электрические цепи. Законы Кирхгофа. Элементы цепи. Идеальные элементы цепей при гармоническом воздействии, страница 4

Строго говоря, все реальные элементы проявляют нелинейные свойства. Однако в определенных интервалах токов и напряжений (малых), мы с большим основанием можем считать их линейными. Приведем примеры проявления нелинейности. Величина обычного сопротивления R зависит от температуры (особенно у полупроводников), а температура - от протекающего тока. Индуктивность катушки с сердечником из ферромагнитных материалов тоже нелинейна, поскольку магнитная проницаемость сердечника зависит от напряженности магнитного поля, определяемой током. В конденсаторах нелинейность проявляется, прежде всего, за счет диэлектрика.

1.7.  Принцип суперпозиции.

Для линейных и параметрических цепей (линейные уравнения) справедлив принцип суперпозиции (наложения). Он значительно упрощает анализ таких цепей и формулируется обычно следующим образом.

Пусть . Здесь: L - линейный оператор, алгебраический или дифференциальный, U - искомое напряжение (или ток), а f определяется источниками. Тогда, если , то задача  имеет решение , где b - константа (пропорциональность). Если  и , то задача  имеет решение  (аддитивность). Последнее свойство легко обобщается на случай любого числа слагаемых.

Упрощение анализа достигается за счет того, что сложный сигнал мы можем представить суммой более простых, стандартных, для которых решение находится проще. Потом все складываем.

1.8.1.  Примеры составления и решения дифференциальных уравнений.

В качестве первого примера, рассмотрим часто используемый двухполюсник, последовательный колебательный контур, рис. 1.6. Надо связать ток в цепи и общее напряжение. Одна величина задана, другая определяется. Ток в элементах одинаковый. Суммируем падения напряжения.

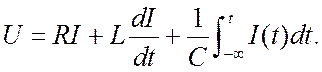 Если задан ток I(t), то вычисляем правую часть этого равенства и получаем напряжение. Если задано напряжение U(t), то после дифференцирования равенства получаем дифференциальное уравнение второго порядка (два накопителя энергии) для тока.

Штрихом будем обозначать производные для упрощения записи. Решение дифференциальных уравнений с постоянными коэффициентами достаточно подробно рассматривается в курсе математики, поэтому мы этим заниматься не будем. Некоторые примеры решений будут рассмотрены позже.

1.8.2.  Теперь рассмотрим параллельный контур, рис. 1.7. Надо связать общий ток и напряжение на конденсаторе. Пишем очевидные равенства:  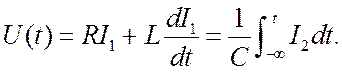  Если задано напряжение U(t), то мы сначала решаем уравнения для  I₁и  I₂.         Затем находим общий ток.

Когда задан общий ток I, то на основании двух предыдущих равенств мы пишем следующие:   Последнее равенство и дает нам дифференциальное уравнение второго порядка для напряжения. 

1.8.3.  Перейдём к четырёхполюснику, рис. 1.8. Оба варианта входной части цепи эквивалентны.  задано, требуется определить . Задаём два тока и выбираем их направление. Затем пишем систему уравнений Кирхгофа.  Нас интересует только ток I₂. Исключая ток I₁, мы получим дифференциальное уравнение второго порядка для тока I₂.  .

1.8.4.  На этом простом примере, рис. 1.9, мы обсудим некоторые общие закономерности. Ключ в схеме помогает рассмотреть ситуацию, когда конденсатор был заряжен до момента подключения генератора. Для этой схемы рассмотрим два случая.

1).  Подключение источника постоянного напряжения  в момент t=0. Пусть , т.е. к моменту включения источника конденсатор был разряжен. При  ключ замыкается, конденсатор заряжается. Можно обойтись в этом случае и без ключа, если считать 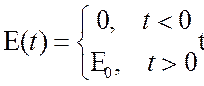. Для области  пишем уравнение. 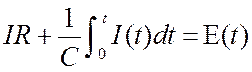 или  , где  - постоянная времени цепи (сек). Можно написать уравнение и для напряжения на конденсаторе . . Левые части уравнений одинаковы.

Если , то получаем однородное уравнение для тока.  (). Напишем сразу его решение  . Как найти ? Надо задать начальные условия, 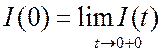. Без дополнительных физических соображений тут не обойтись.