Механизмы поляризации диэлектриков. Мультипольное разложение. Электронная поляризация молекул, страница 4

	(4.19)	Наиболее общая связь между вектором дипольного момента и полем в случае анизотропных молекул с электронным механизмом поляризации.
	(4.20)	Дипольный момент неполярной анизотропной молекулы с линейной поляризуемостью во внешнем поле.
	(4.21)	Компактная запись соотношений (4.20).

Пример 4.4. :    Тензор поляризуемости линейной молекулы.

Рассчитать тензор поляризуемости линейной молекулы, дипольный момент которой всегда направлен вдоль молекулярной оси, положение которой в пространстве задано (рис.4.3). Величина поляризуемость молекулы при ориентации ее оси по полю известна: a_l.

Решение:           

Величина дипольного момента молекулы определяется проекцией электрического поля на молекулярную ось (4.22). Х - компонента наведенного дипольного момента определяется в результате проектирования вектора d на координатную ось (4.23). Коэффициент пропорциональности между этой проекцией и х - составляющей электрического поля является первым элементом матрицы искомого тензора (4.24). Остальные матричные элементы рассчитываются аналогично.

              Полученная описанным способом матрица тензора поляризуемости линейной молекулы оказывается симметричной относительно диагонали и,  следовательно, может быть приведена к диагональному виду соответствующим поворотом системы координат.  Далее будет показано, что таким свойством обладает тензор поляризуемости произвольной молекулы.

	Рис. 4.3	Анизотропная неполярная молекула во внешнем электрическом поле.
	(4.22)	Проекция внешнего поля на молекулярную ось.
	(4.23)	х - компонента дипольного момента анизотропной молекулы.
	(4.24)	Один из девяти элементов матрицы тензора поляризуемости линейной молекулы.

Задачи для самостоятельного решения

4.1.   Определить зависимость от расстояния между частицами силы электростатического взаимодействия между а) двумя диполями; б) ионом и неполярной молекулой; в) диполем и неполярной молекулой. Рассмотреть случаи, когда диполи ориентированы вдоль прямой, соединяющей взаимодействующие частицы и перпендикулярны этой прямой. Указание: учесть малость размеров молекулярных систем по сравнению с расстояниями между ними. Результат решения задач не должен содержать каких-либо характеристик молекул, кроме их полных зарядов, дипольных моментов и поляризуемостей.

4.2.   Рассчитать энергию ионизации атома Томсона. Заряд ядра и радиус электронного облака известны.

4.3.   Рассчитать линейную поляризуемость атома гелия, распределение электронной плотности, в котором описывается формулой  (4.8).

4.4.   Рассчитать величину константы линейной ориентационной поляризуемости газа из молекулярных диполей с моментом d₀ при заданной температуре Т. Указание: разложить выражение (4.18) для среднего дипольного момента дипольной молекулы в ряд Тейлора вблизи точки Е=0.

4.5.   Найти все элементы матрицы поляризуемости линейной молекулы, изображенной на рис. 4.3.

4.6.   Рассчитать средний дипольный момент для газа из “полностью анизотропных” линейных молекул, способных поляризоваться лишь в одном направлении (вдоль молекулярной оси), если температура газа равна Т. Считать заданной поляризуемость молекулы при ее ориентации точно по полю (a₀).

         Указание: при записи функции распределения учесть, что помещенная в электрическое поле молекула помимо электростатической энергии взаимодействия ее дипольного момента с полем обладает дополнительной потенциальной энергией деформации.

4.7* Рассчитать средний дипольный момент для случая помещенного в заданное внешнее электрическое поле газа из полярных молекул с линейной поляризуемостью, определяемой тензором вида:

         .

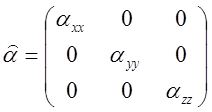Соотношения, которые полезно помнить
	Наведенный внешним полем дипольный момент молекулы (линейное приближение).
	Энергия диполя во внешнем поле.