Pa =M s-0,25 / r-r0
Здесь М-молекулярный вес жидкости, r - плотность, r0 - плотность пара,
При температуре далекой от критической зависимость упрощается
Pa =Vm s -0,25
Vm- объем грамм-молекулы. При s =1 парахор численно равен молекулярному объему.
Для насыщенных углеводородов парахор можно рассчитать по простой формуле
Pa = 39 n + 34,2
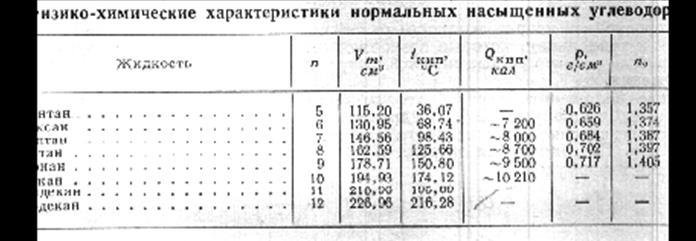
Теоретические значения с точностью до нескольких процентов совпадают с экспериментальными. Парахор величина аддитивная и определяется путем сложения величин парахоров отдельных связей. Так например для группы СН2 парахор равен 39, для группы CH3 - 56,1
Для соединений типа CH3 (CH2)n = CH3 парахор можно рассчитать по формуле
Pa = 2 * 56,1 + n * 39
 |
Мольная рефракция R также является аддитивной величиной
R = M (n2 +1)/ (n2 -1) r
n-в этой формуле коэффициент преломления, а не число атомов углерода.
Численные значения коэффициента рефракции можно вычислить по значениям C и H. Например для атома углерода С Rc = 2,418, для атома водорода H Rh = 1,11, следовательно для группы CH2 R CH2 =2,418 + 2,222 = 4,638, а для группы CH3
R CH3 = 5,748.
Для соединений типа CH3 ( СH2)x=CH3 мольная рефракция вычисляется по формуле
R = 2 (CH3) + x (CH2) = 4,64 x + 11,5
Как известно теория жидкости наталкивается на большие трудности, в особенности для жидкостей с многоатомными молекулами. Однако в некоторых случаях удалось вывести зависимости свойств жидкости от структуры молекул, исходя из полуэмпирических соображений, или из законов термодинамики или стат-физики. С точки зрения электрофизики жидкости эти зависимости позволяют установить взаимосвязь некоторых электрофизических свойств жидкости, таких как проводимость, коэффициенты диссоциации и рекомбинации молекул, их подвижности, а также величины пробивных напряжений с молекулярной структурой.
Рассмотрим некоторые результаты, касающиеся группы насыщенных углеводородов. Например в работах Курата и Исиды получены следующие соотношения для температуры кипения Тk для углеводородов типа Сn H2n+2.
Тk=(0,00057+0,00775/n2/3. (1)
Здесь n-характеризует число молекул водорода в молекуле углеводорода. Формула достаточно хорошо описывает экспериментальные данные. У Адамчевского приведены полуэмпирические формулы описывающие зависимость температуры кипения и плавления Тпл. для парафиновых углеводородов.
Тк=146*n1/2-17 (2)
Tп=67*n1/2+18 (3)
Например для гексана n=6, Тк=3410К, Тп=1780К.
Эти формулы дают хорошее соответствие с экспериментальными данными при 4<n<17. Для n=1,2,3,4 т.е. для углеводородов находящихся в нормальных условиях в газообразном состоянии, отклонения большие. При использовании формулы (1) таких отклонений нет.
На рис. представлены зависимости температур кипения и плавления углеводородов типа Сn H2n+2. Жидкое состояние соответствует заштрихованной области. Адамчевским, полуэмпирическим путем, получены формулы (4) и (5), описывающие зависимость плотности парафинов и их вязкости от числа n. Молекулярный вес жидких парафинов М=14,026*n+2,01626 .
Плотность при комнатной температуре равна
R=14,026*n+2,01626/16*(n+2,27), г/см3. (4)
Плотность при температуре t равна
R=14,026*n+2,01626/16*(n+2,27)*(1+0,0194*t/n+8) (5)
Вязкость жидкости.
Вязкость жидкости играет важную роль в процессах миграции ионов, электрогидродинамических течениях, процессах диффузии и рекомбинации ионов. Существует несколько теорий вязкости жидкости. Адамчевским получена формулы для насыщенных углеводородов, достаточно хорошо соответствующие эксперименту. Для значений 4<n<17 хорошо работает формула 6, для 28<n<64, работает формула 7.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.