Межмолекулярные силы в жидкостях и их физико-химические свойства, страница 4

ΔV/V=β ΔT                                                               

где DT — изменение температуры и β — коэффициент объемного расширения, т. е. относительное изменение объема, приходящееся на один Кельвин. Полагая ΔV =V— V₀, где V₀ — объем тела при температуре tо=0°С, а ΔΤ=t—t₀=t, имеем

(V-V₀)/Vo= β t                                                                                 

Линейный  закон теплового расширения — это первое приближение, справедливое лишь в определенном ин­тервале температур, зависящем от свойств вещества. При расши­рении интервала температур линейность нарушается. Так, напри­мер, нарушение линейности легко обнаружить у воды при темпе­ратуре около 4°С, когда она имеет максимальную плотность, а при охлаждении ниже 4°С она начинает расширяться вплоть до точки замерзания.

Кроме того, как 'следует из теории и подтверждается в экспе­рименте, вблизи абсолютного нуля тепловое расширение отсутст­вует практически у всех веществ.

Зависимость физико-химических свойств жидкости от структуры молекул.

 

                  Поверхностное натяжение, мольная рефракция.

    Как известно поверхностное натяжение равно работе, необходимой для того, чтобы увеличить вдвое 1 см²   свободной поверхности жидкости, или разделить надвое некоторый объем жидкости с поперечным сечением в 1 см².

      По Ленард-Джонсону результирующая взаимодействия между двумя молекулами равна сумме сил притяжения F₁ и отталкивания  F₂

                            F₁=-a/ r⁷

                             F₂= b/ r¹³                     F=F₁ + F₂

где r- расстояние между молекулами.

Энергия связи двух молекул равна работе необходимой для их разделения A_m

                                   A_m=a/6 r⁶

Чтобы разделить два тела с поперечным сечением  1 см² необходимо произвести работу

                                    A₂= K a/ 6 r⁶

По определению А₂=2s, И СЛЕДОВАТЕЛЬНО

                               s=K а/ 12 r⁶

 

Численное значение поверхностного натяжения можно найти измеряя высоту подъема жидкости в капилляре

                                  s 2 p = p r² h g r

здесь r плотность жидкости

                                           s = r h g r/ 2      

Итак по величине поверхностного натяжения можно судить о среднем расстоянии между молекулами r.

  Величину поверхностного натяжения можно определить, также с помощью сталагмометра измеряя количество капель-n, находящихся в некотором объеме V. Поскольку капля отрывается, когда ее вес становится больше сил поверхностного натяжения, то

                                              s = V g r/ K n 

здесь К- постоянная прибора, n-количество капель в объеме V.

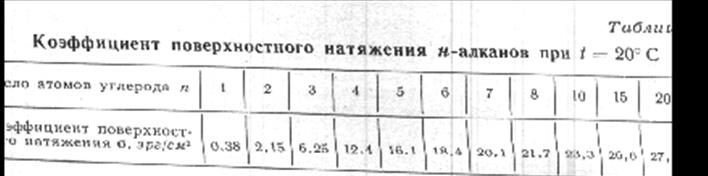
Теоретические расчеты поверхностного натяжения для н-алканов показали хорошее совпадение с экспериментом. В таблице приведены значения  s для н-алканов.

Вычислить величину поверхностного натяжения для углеводородов от числа атомов углерода n в молекуле можно по формуле

.

                                                   s= 7,17+ 2,19 n + 0,056 n²

Кроме того имеются зависимости поверхностного натяжения от температуры:

                                           s = s₀( 2,929 - 1,929 T/T₀ )

где Т₀=Т₁+0,5 t_кип.

t_кип- температура кипения.

Аналогичные уравнения исходя из теории подобия получены для теплопроводности l, плотности r и теплоемкости С

                                     l= l₀ [1,575 - 0,05588 Т/T₀ - 0,0179 (T/T₀)²]

                                     l =l₀ ( 1,6 n + 0,20) 

                                    r= r₀[ 1,3932 - 0,3757 T/T₀ - 0,0414 ( T/T₀)²]

                                     r =  r₀ (  11,87 n - 14,80)  

Эти полуэмпирические формулы достаточно хорошо соответствуют экспериментальным данным.

Одной из важных характеристик жидкости является парахор. Он является аддитивной величиной для различных атомов и связей в молекулах и имеет отношение к поверхностному натяжению жидкости.

  Парахор P_a связан с поверхностным натяжением  следующим соотношением