




2.2 Дискретные сигналы
Связь спектров аналогового и дискретного сигналов (1-131)
Аналоговый
сигнал ![]() .
.
Отсчеты
аналогового сигнала ![]()
![]() .
.
Идеальный
тактирующий сигнал 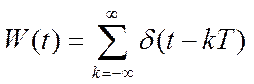 . (Домножение на
. (Домножение на ![]() - функцию изменяет размерность исходного
выражения).
- функцию изменяет размерность исходного
выражения).
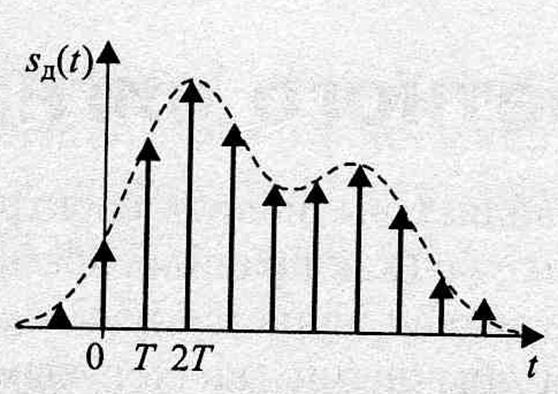
Рис.3.4.
Дискретный сигнал представляем в виде произведения исходного аналогового сигнала на тактирующий сигнал
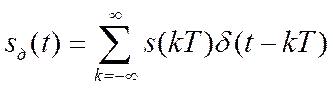
Так как дельта-функция = 0 везде, кроме t=kT, то можно (1) записать в виде произведения аналогового и тактирующего сигналов.
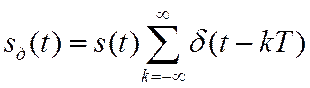
Тактирующий сигнал – периодическая функция, поэтому
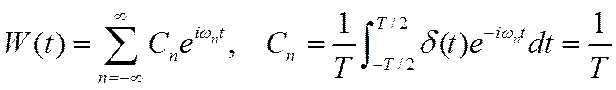 .
.
Следовательно,
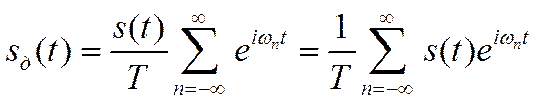
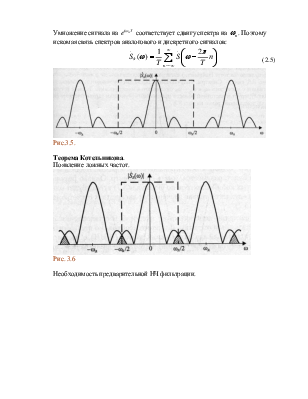
Умножение сигнала на ![]() соответствует сдвигу спектра на
соответствует сдвигу спектра на ![]() . Поэтому искомая связь спектров
аналогового и дискретного сигналов:
. Поэтому искомая связь спектров
аналогового и дискретного сигналов:
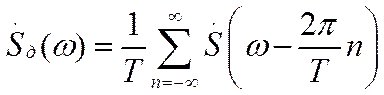
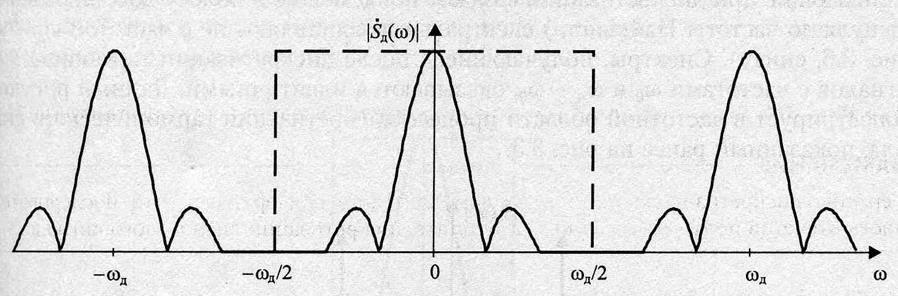
Рис.3.5.
Теорема Котельникова.
Появление ложных частот.
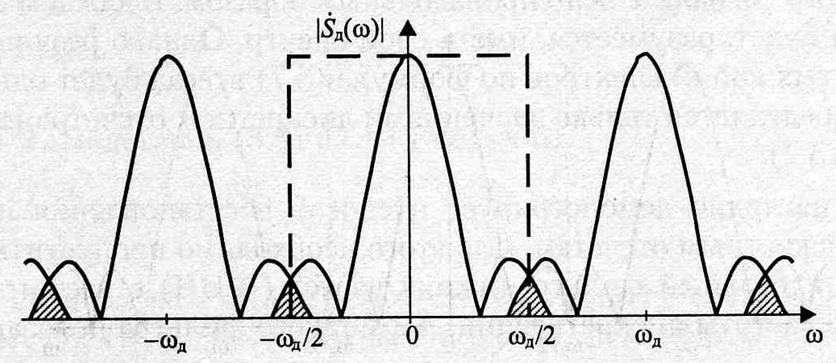
Рис. 3.6
Необходимость предварительной НЧ фильтрации.
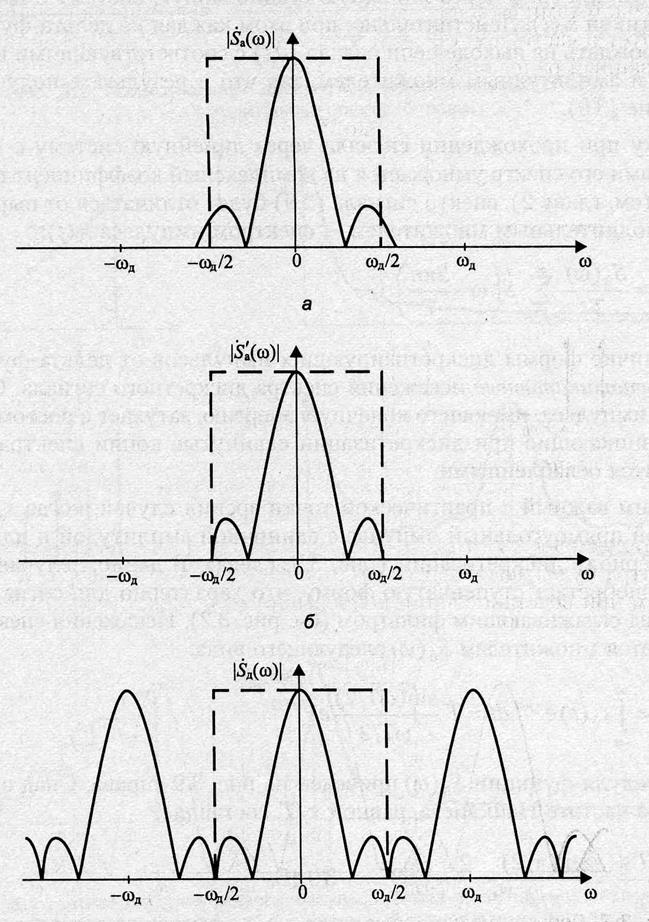
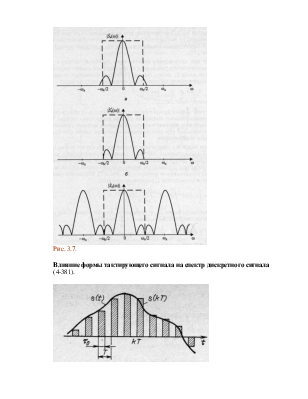
Рис. 3.7.
Влияние формы тактирующего сигнала на спектр дискретного сигнала (4-381).
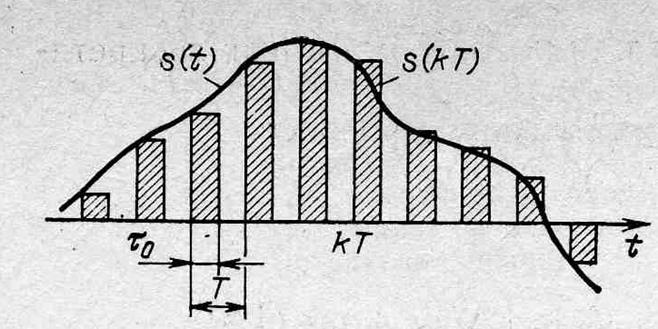
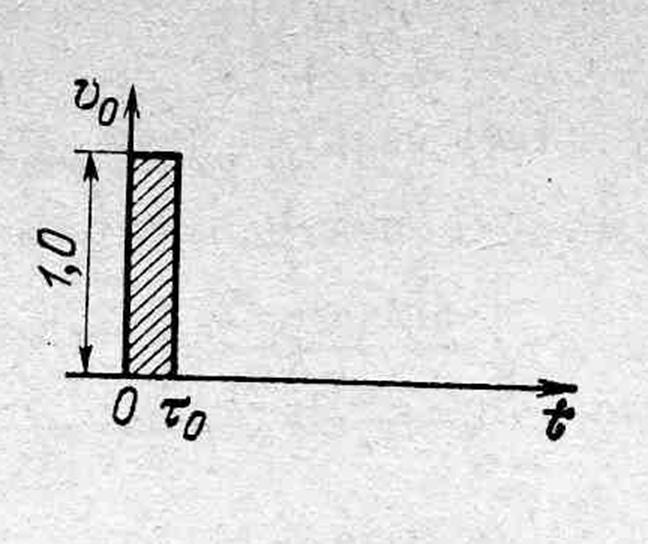
Рис. 12.31, 12.32
Тактирующий импульс ![]() определен на интервале от 0 до Т и =0 вне
этого интервала. Его длительность
определен на интервале от 0 до Т и =0 вне
этого интервала. Его длительность ![]() .
.
Тактирующий сигнал ![]() сумме тактирующих импульсов.
сумме тактирующих импульсов.
Отдельный импульс
прямоугольной формы амплитуды s(kT) и длительности Т можно представить как свертку ![]() .
.
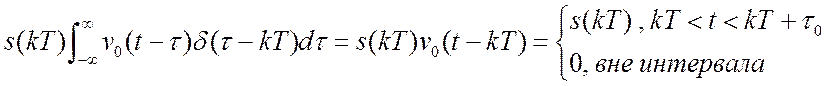
Тогда
![]()
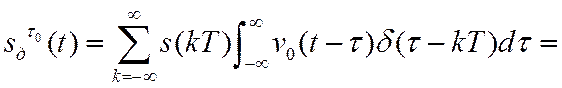
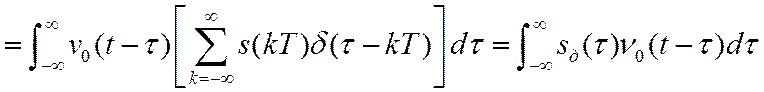
Следовательно, спектры сигналов связаны следующим образом
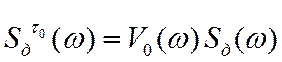
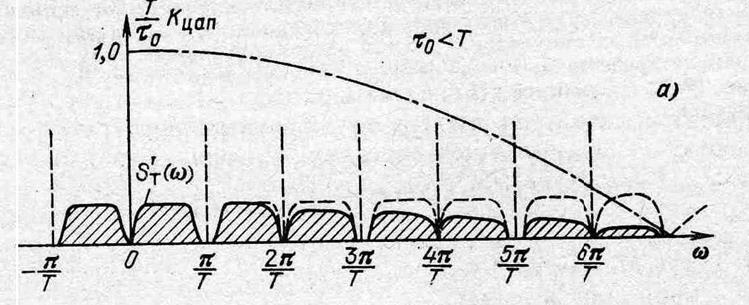
Рис. 12.33 (Лучше С.3-10)
Задание. Рассчитать искажение спектра дискретного сигнала при
дискретизации тактирующим сигналом прямоугольной формы для ![]() и
и ![]() .
.
Преобразование Лапласа и Фурье от дискретного сигнала (1-145), (2-147).
Преобразование Лапласа (для одностороннего сигнала)
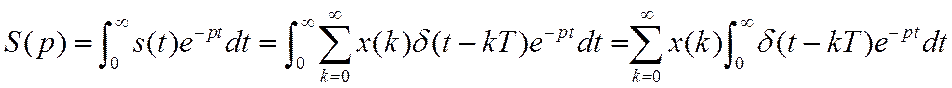
Таким образом,
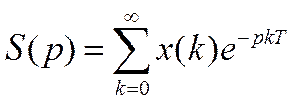
Спектр, как и сам сигнал, полностью определяется своими отсчетами.
Иногда аргумент спектральной функции записывают в виде
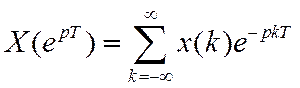
подчеркивая тем самым, что
спектр зависит не от p или![]() непосредственно, а от комбинации
непосредственно, а от комбинации ![]() .
.
Преобразование Фурье
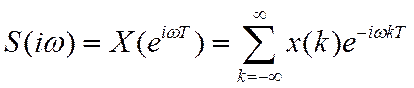
Задание. Вычислить спектр дискретного сигнала ![]() .
.
Свойства спектров дискретных сигналов (2-147).
Дискретное преобразование Фурье
Было: спектр ДС
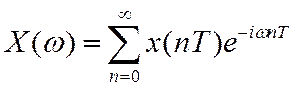
![]() -
бесконечная последовательность,
-
бесконечная последовательность,
![]() -
непрерывная периодическая функция с периодом
-
непрерывная периодическая функция с периодом ![]() .
.
Так же для конечных последовательностей
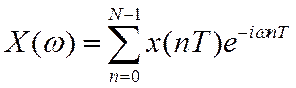
ДПФ бесконечной периодической последовательности
Аналоговый периодический
сигнал ![]() с периодом
с периодом ![]() может
быть представлен рядом Фурье
может
быть представлен рядом Фурье
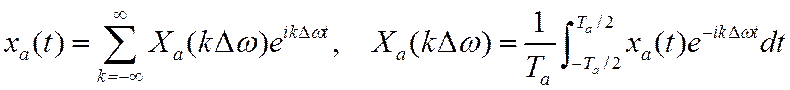 ,
,
где 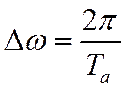
Аналогично дискретный
периодический сигнал ![]() с периодом
с периодом ![]()
![]()
можно представить рядом
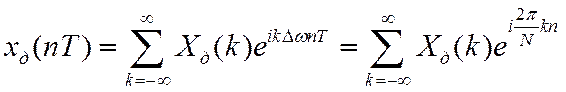 .
.
Здесь проведены замены
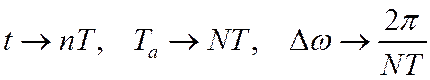 .
.
Для нормированного времени
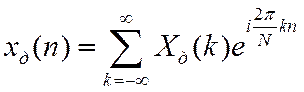 ,
,
где ![]() -
номер отсчета, соответствующий частоте
-
номер отсчета, соответствующий частоте 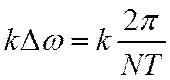 .
.
Спектр ![]() периодической последовательности
периодической последовательности ![]() определяется суммой
определяется суммой
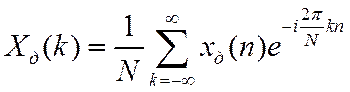
Заметим, что в (5) и (7)
экспоненты 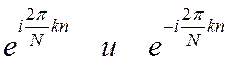 - периодические
функции как по
- периодические
функции как по ![]() , так и по
, так и по ![]() с одним и тем же периодом
с одним и тем же периодом ![]() . Следовательно, периодическим является не
только дискретный сигнал, но и его спектр. В выражениях (6) и (7) мы можем
ограничиться частичными суммами (в пределах периода) и записать пару ДПФ в виде
(множитель
. Следовательно, периодическим является не
только дискретный сигнал, но и его спектр. В выражениях (6) и (7) мы можем
ограничиться частичными суммами (в пределах периода) и записать пару ДПФ в виде
(множитель ![]() обычно ставится не в (7), а в (6)):
обычно ставится не в (7), а в (6)):
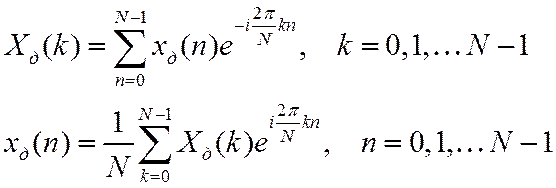
Пара преобразований (8) называется прямым и обратным ДПФ периодической последовательности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.