Структурные схемы систем автоматического управления. Устойчивость линейных САУ

5. СТРУКТУРНЫЕ   СХЕМЫ   СИСТЕМ   АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

5.1. Элементы структурных схем

Для графического изображения автоматических систем и их математических моделей используются схемы различных типов: принципиальные, структурные и функциональные (ГОСТ 791-68). Структурная схема определяет основные   функциональные части системы, их назначение и взаимосвязь. Все элементы на ней изображаются в виде блоков. Свойства блоков могут быть раскрыты различным образом, в связи с чем существует несколько разновидностей структурных схем: алгоритмические, конструктивные и т.д. Наиболее распространенной формой математического описания в ТАУ стали алгоритмические  структурные схемы, отражающие динамические свойства САУ.

Структурная схема – это графическое изображение элемента или САУ, отображающее систему дифференциальных уравнений, которые описывают процессы управления в этих элементах.

Структурные схемы содержат элементы, которые изображаются следующим образом.

1.  Динамические звенья (рис. 5.1).

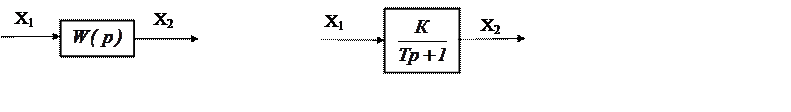
Рис. 5.1

2.  Элементы сравнения или сумматоры.

Для суммирования  сигналов  Х₁+Х₂=Х₃ существует два варианта изображения (рис. 5.2):

 

 

 

             

Рис. 5.2

Для вычитания сигналов   Х₁–Х₂=Х₃   применяют изображения

(рис. 5.3).

 

 

 

 

 

Рис. 5.3

3. Узлы разветвления сигналов (рис. 5.4), для которых справедливо равенство  Х₁=Х₂=Х_3.

 

              

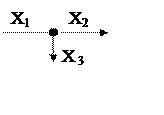Рис.  5.4

В структурных схемах предполагают, что все звенья преобразуют сигнал в одном направлении и передаточные функции отдельных звеньев не зависят от способа их соединения.

5.2. Типовые  соединения  звеньев

Последовательное соединение звеньев

Передаточная функция последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев. Эквивалентная передаточная функция звеньев, представленных на рис. 3.25, будет равна:

 

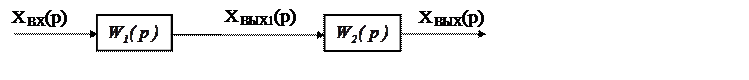Рис. 5.5

_.

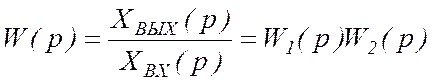Параллельное соединение звеньев

Передаточная функция параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев. Эквивалентная передаточная функция звеньев, приведенных на рис. 5.6, будет равна:

 

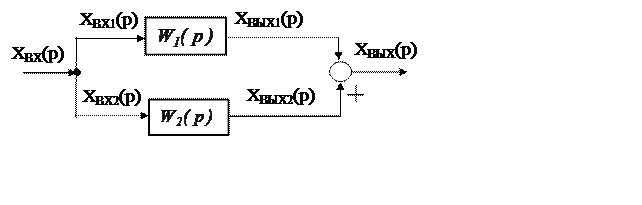
Рис.  3.6

Рис. 5.6

_.

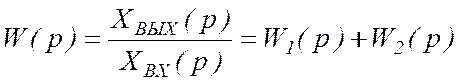Звено с обратной связью или

(встречно-параллельное соединение звеньев)

Схема соединения звеньев изображена на рис. 5.7.

Передаточная функция звена, охваченного отрицательной (положительной) обратной связью, равна передаточной функции прямой цепи, деленной на единицу плюс (минус) произведение передаточной функции прямой цепи и передаточной функции цепи обратной связи.

 

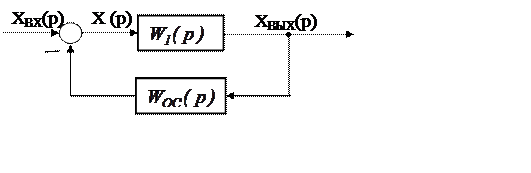Рис. 5.7

.

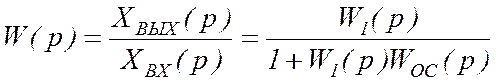5.3. Правила  преобразования структурных  схем

Преобразование структурных схем применяется для определения передаточных функций сложных структурных схем, к которым нельзя непосредственно применить правила для типовых соединений звеньев.

Правила переноса узлов разветвления

1. Перенос узла разветвления с выхода звена на его вход (рис. 5.8) требует включения согласующего звена с передаточной функцией W(p).

 

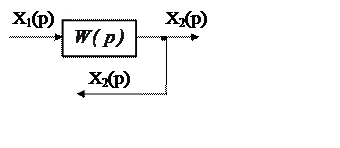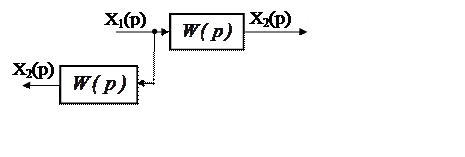Рис. 5.8

2. Перенос узла разветвления с входа звена на выход (рис. 5.9) требует включения согласующего звена с передаточной функцией 1/W(p).

 

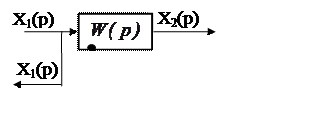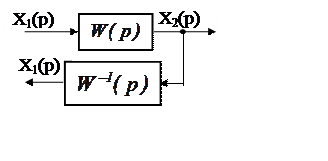Рис. 5.9

Правила переноса узлов суммирования

1. Перенос сумматора с выхода звена на его вход (рис. 5.10)  требует включения согласующего звена с передаточной функцией 1/W(p).

 

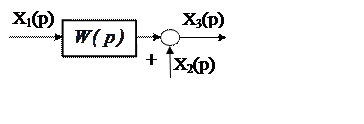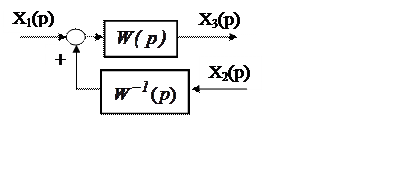Рис. 5.10

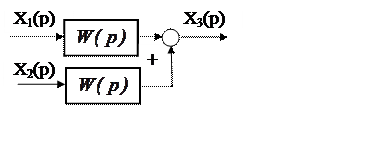
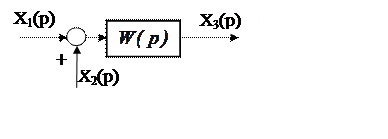2. Перенос сумматора с  входа звена на его выход (рис. 5.11)  требует включения согласующего звена с передаточной функцией  W(p).

Рис. 5.11

3.  Перемена местами узла разветвления и сумматора (рис. 5.12)

 

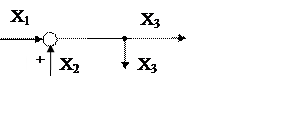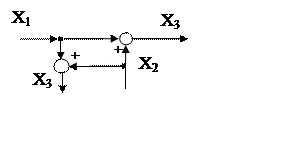Рис. 5.12

Пример 5.1. Дана структурная схема системы (рис. 5.13). Определить передаточную функцию  между переменными Х_ВХ(р) и Х_ВЫХ(р).

 

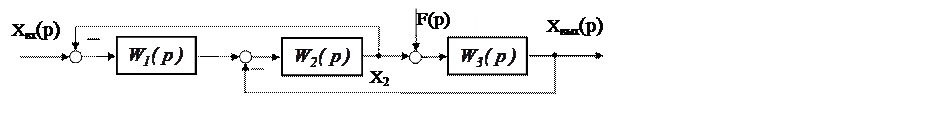Рис.  5.13

Положим F = 0 и перенесем узел разветвления с входа звена W₃(p) на его выход и получим преобразованную схему на рис.  5.14 .

 

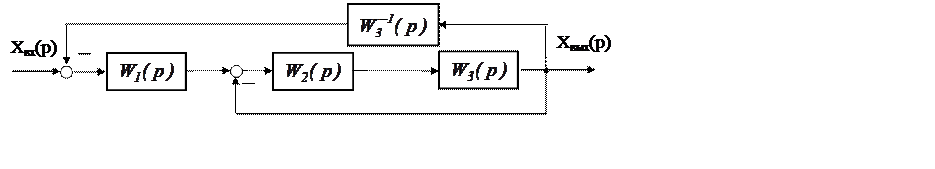
Рис.  5.14

Найдем передаточную функцию замкнутого контура с единичной обратной связью

,

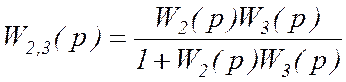тогда схема примет вид на рис.  5.15.

 

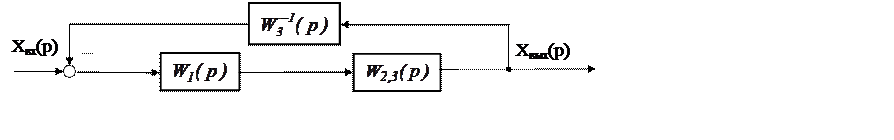Рис.  5.15

Искомая  передаточная функция будет равна:

.

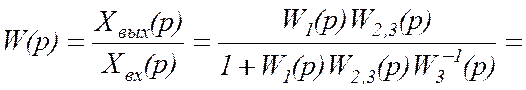
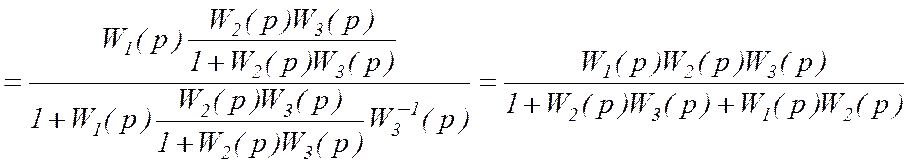Пример 5.2. Дана функциональная схема системы стабилизации скорости вращения  двигателя постоянного тока. Требуется составить структурную схему системы и определить передаточные функции.

          Для каждого элемента системы находим передаточную функцию типового динамического звена и изображаем их на структурной схеме в той же последовательности как на функциональной схеме. Передаточные функции усилителя (У) - W_y(p), тиристорного преобразователя (ТП) - W_тп(р), двигателя постоянного тока с независимым возбуждением - W_д(p) и тахогенератора (ТГ), являющегося  датчиком обратной связи, - W_тг(р ) имеют  вид: