Министерство образования и науки
Московский государственный университет леса
Кафедра УАП ЛПК

Лабораторная работа №5 по ТАУ:
Анализ устойчивости САР по расположению корневых точек и критерию Михайлова в среде MATLAB
Выполнил: студент группы АП-31
Морозов А. Е.
Проверил: Дорошенко В. А.
Москва 2010
Содержание:
1. Исходные данные.
2. Определение устойчивости САР по расположению корневых точек на корневой плоскости.
3. Определение устойчивости САР по критерию Михайлова.
1. Исходные данные:
1. Структурная схема системы регулирования:
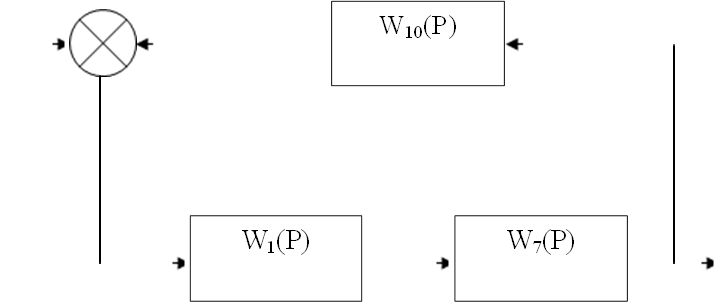 |
2. Передаточные функции системы регулирования:
W10(P)=2,0
W1(P)=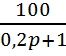
W7(P)=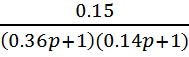
Время переходного процесса 2с.
Перерегулирование 20%
3. Передаточная функция замкнутой системы регулирования без корректирующего звена:
Wz=
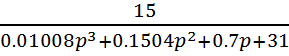
4. Передаточная функция корректирующего звена:
W=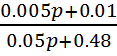
5. Передаточная функция замкнутого звена с учетом корректирующего звена:
Wz=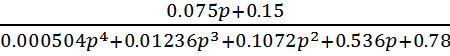
2. Определение устойчивости САР по расположению корневых точек на корневой плоскости.
2.1. Определение устойчивости САР без корректирующего звена.
2.1.1. Определение корней характеристического полинома.
Wz=
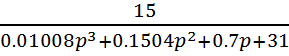
P=![]()
>> P=[0.01008 0.1504 0.7 31]
P =
0.0101 0.1504 0.7000 31.0000
>> roots(P)
ans =
-19.4680
2.2737 +12.3613i
2.2737 -12.3613i
2.1.2 График распределения корней:
>> sys1=tf([0.01008 0.1504 0.7 31],[0 1])
Transfer function:
0.01008 s^3 + 0.1504 s^2 + 0.7 s + 31
>> pzmap(sys1)
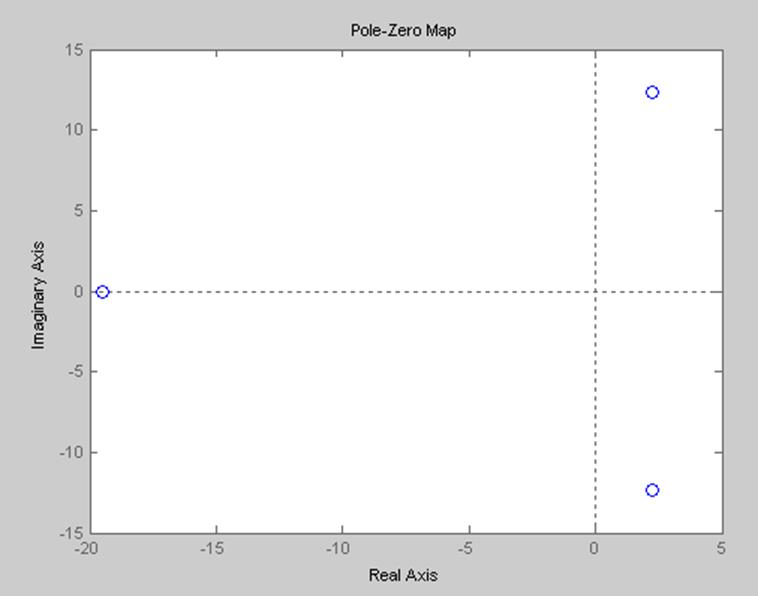
2.1.3 График непрерывной временной характеристики САР.
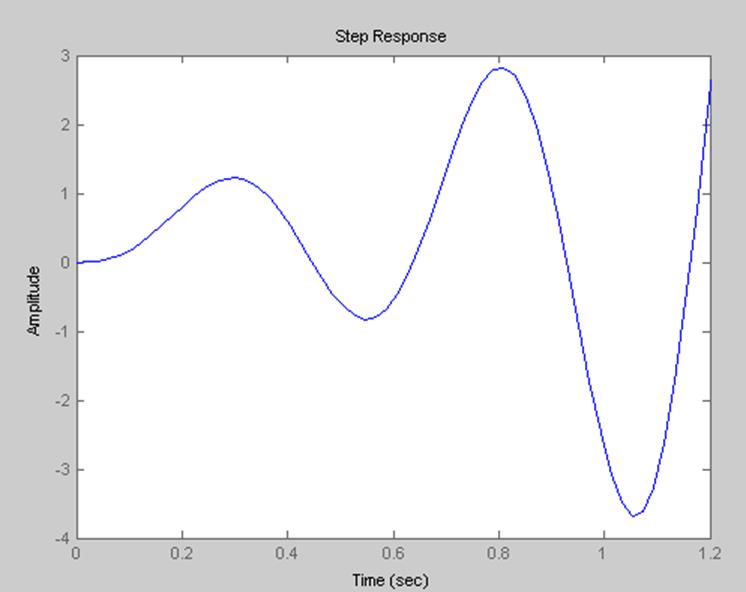
Система неустойчива, т.к. не все корни на корневой плоскости расположены слева от мнимой оси.
2.2. Определение устойчивости САР с корректирующим звеном.
2.2.1. Определение корней характеристического полинома.
Wz=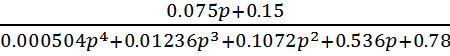
P=![]()
>> P=[0.000504 0.01236 0.1072 0.536 0.78]
P =
0.0005 0.0124 0.1072 0.5360 0.7800
>> roots(P)
ans =
-14.3369
-3.9938 + 5.7560i
-3.9938 - 5.7560i
-2.1993
2.2.2. График распределения корней.
>> sys2=tf([0.000504 0.01236 0.1072 0.536 0.78],[0 1])
Transfer function:
0.000504 s^4 + 0.01236 s^3 + 0.1072 s^2 + 0.536 s + 0.78
>> pzmap(sys2)
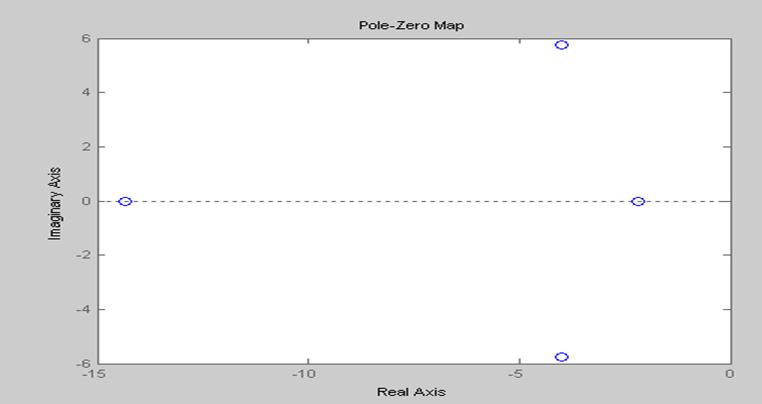
2.2.2. График непрерывной временной характеристики САР с корректирующим звеном.
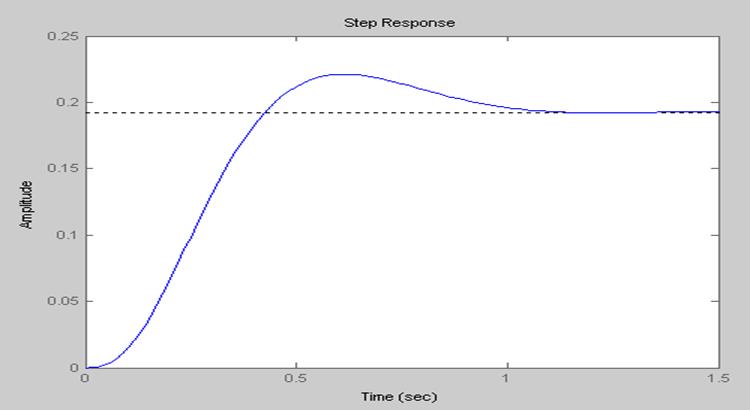
Система устойчива, т.к. все корни на корневой плоскости расположены слева от мнимой оси.
2.3. Определение устойчивости САР по полиному без свободного члена.
2.3.1. Определение корней характеристического полинома.
Wz=
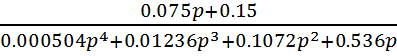
P=![]()
>> P=[0.000504 0.01236 0.1072 0.536 0]
P =
0.0005 0.0124 0.1072 0.5360 0
>> roots(P)
ans =
0
-15.1030
-4.7104 + 6.9446i
-4.7104 - 6.9446i
2.3.2. График распределения корней.
>> sys3=tf([0.000504 0.01236 0.1072 0.536 0],[0 1])
Transfer function:
0.000504 s^4 + 0.01236 s^3 + 0.1072 s^2 + 0.536 s
>> pzmap(sys3)
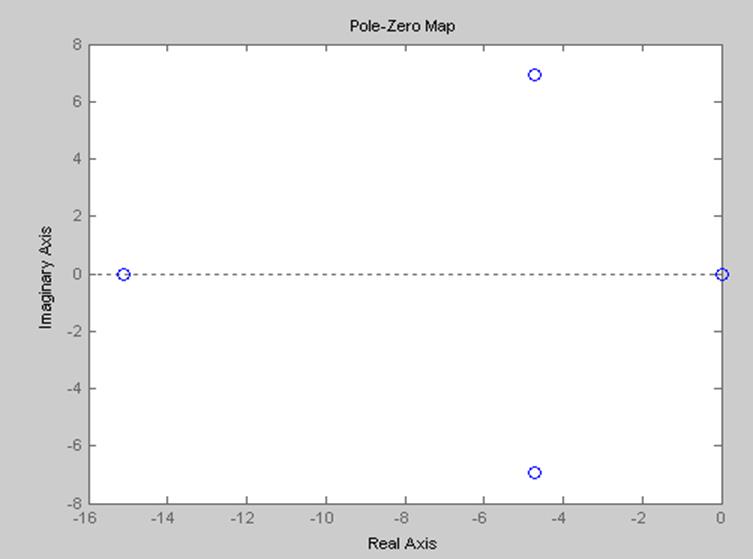
2.3.3. График непрерывной временной характеристики.
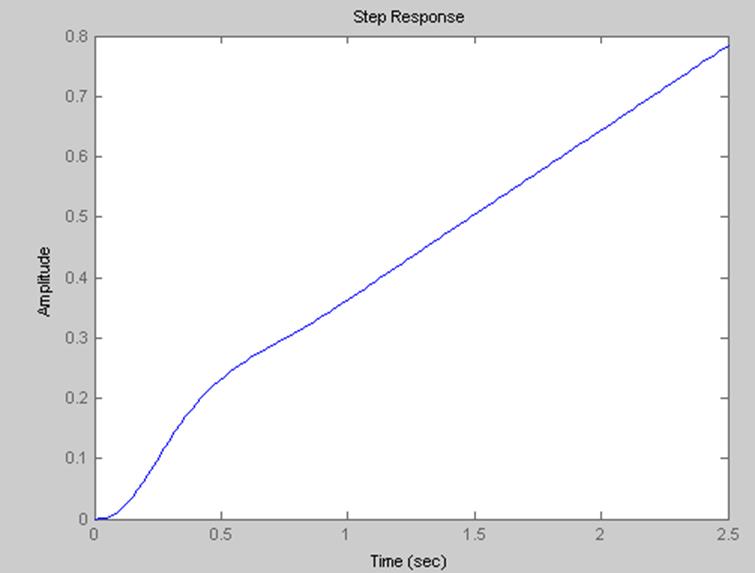
Система находиться на грани устойчивости, т.к. один корень находиться в начале координат.
3. Определение устойчивости по критерию Михайлова.
3.1. Определение устойчивости по критерию Михайлова без корректирующего звена.
3.1.1Построение гадографа Михайлова.
Wz= 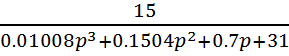
D=![]()
D=![]()
Re=![]()
Im=![]()
num=[0.01008 0.1504 0.7 31];
den=[1];
w=0:15;
apk=freqs(num,den,w);
u=real(apk);
v=imag(apk);
>> plot(u,v);grid
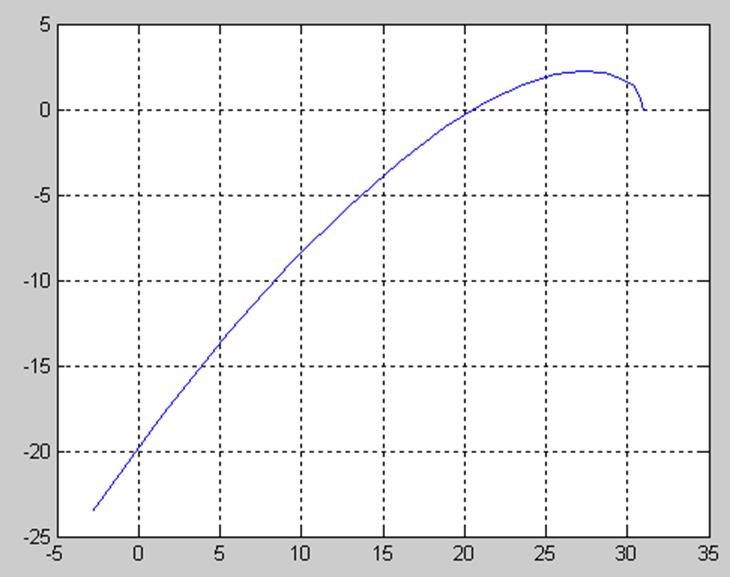
3.1.2 Построение временных переходных характеристик.
Непрерывная временная характеристика.
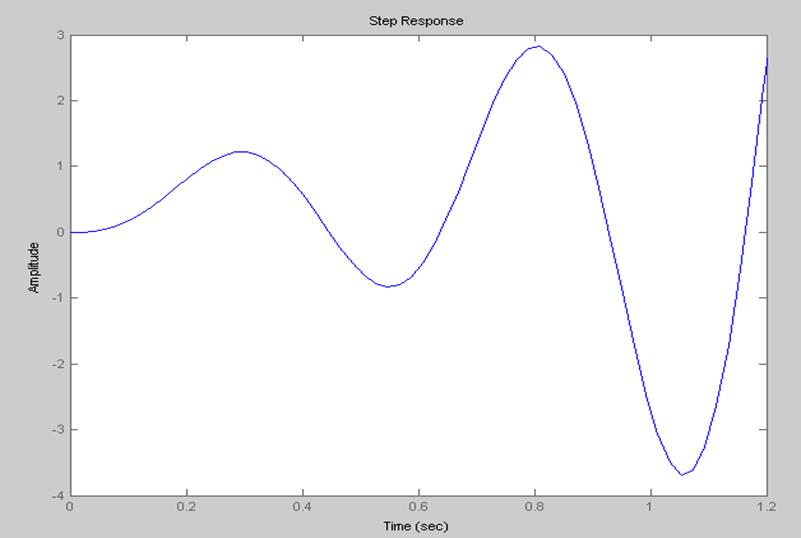
Импульсная переходная характеристика.
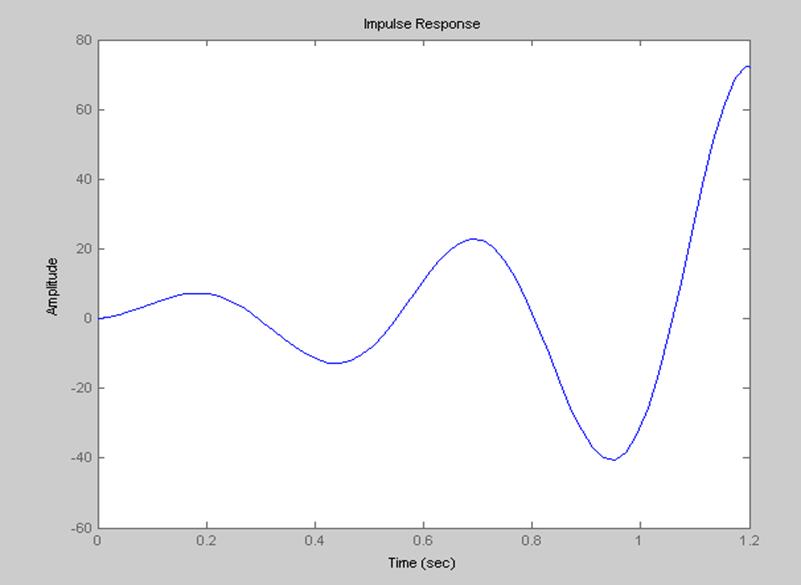
Система неустойчива, т.к. график не проходит последовательно 3 квадранта.
3.2. Определение устойчивости по критерию Михайлова с учетом корректирующего звена.
3.2.1 Построение гадографа Михайлова
Wz=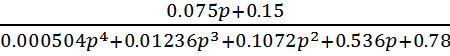
D=![]()
D=![]()
Re=![]()
Im=![]()
>> num=[0.000504 0.01236 0.1072 0.536 0.78];
>> den=[1];
>> w=0:20;
>> apk=freqs(num,den,w);
>> u=real(apk);
>> v=imag(apk);
>> plot(u,v);grid
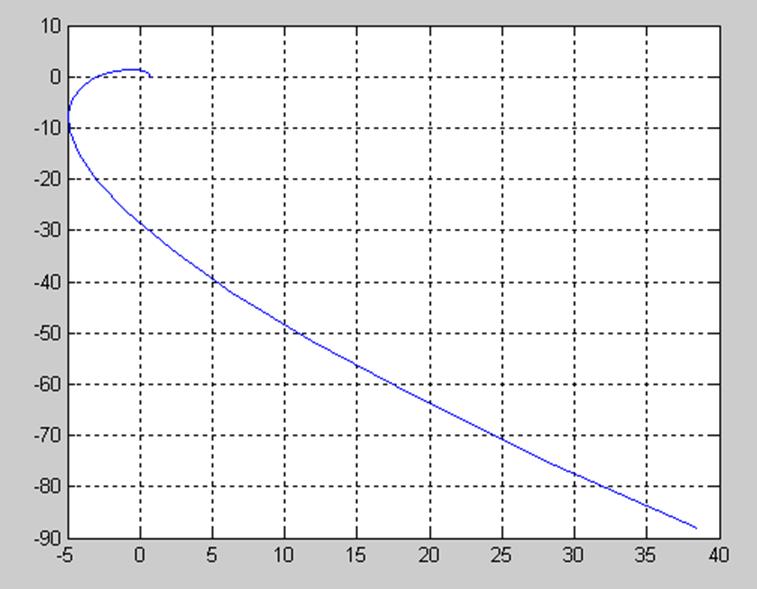
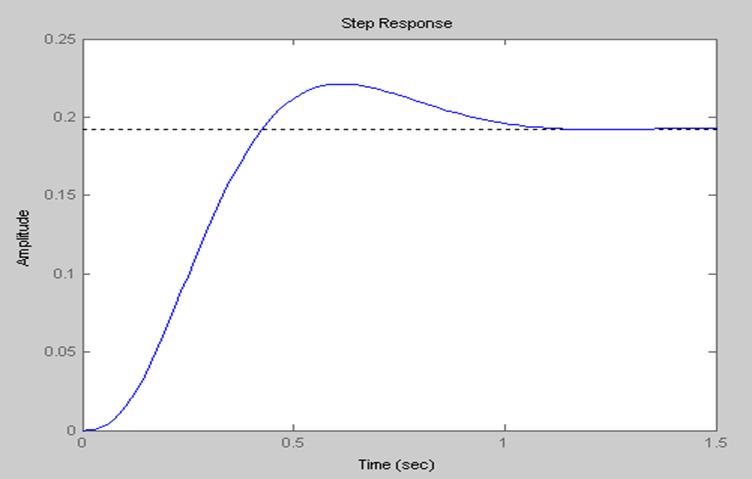
3.2.2. Построение временной переходной характеристики.
Непрерывная временная характеристика.
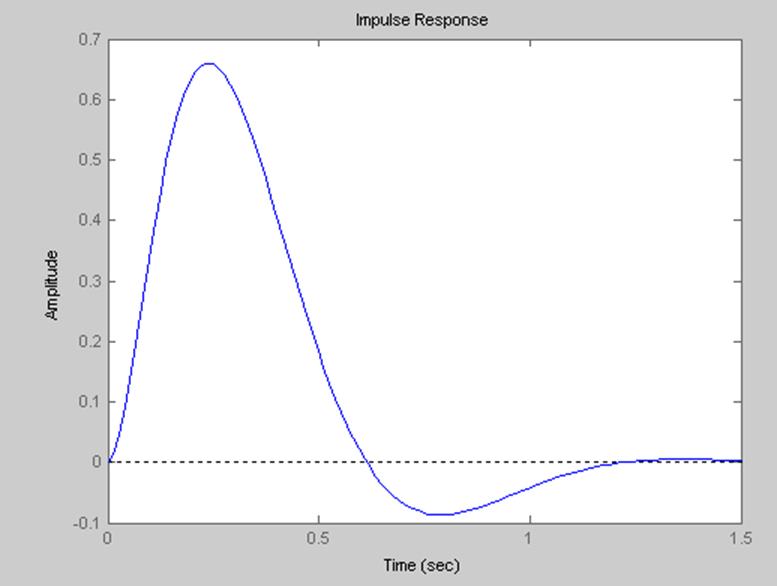
Импульсная временная характеристика.
Система устойчива, т.к. график вращается против часовой стрелки, проходит последовательно 4 квадранта и не пересекает начало координат.
3.3 Определение устойчивости без свободного члена характеристического полинома.
3.3.1 Построение гадографа Михайлова.
Wz=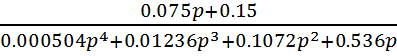
D=![]()
D=![]()
Re=![]()
Im=![]()
>> num=[0.000504 0.01236 0.1072 0.536 0];
>> den=[1];
>> w=0:20;
>> apk=freqs(num,den,w);
>> u=real(apk);
>> v=imag(apk);
plot(u,v);grid
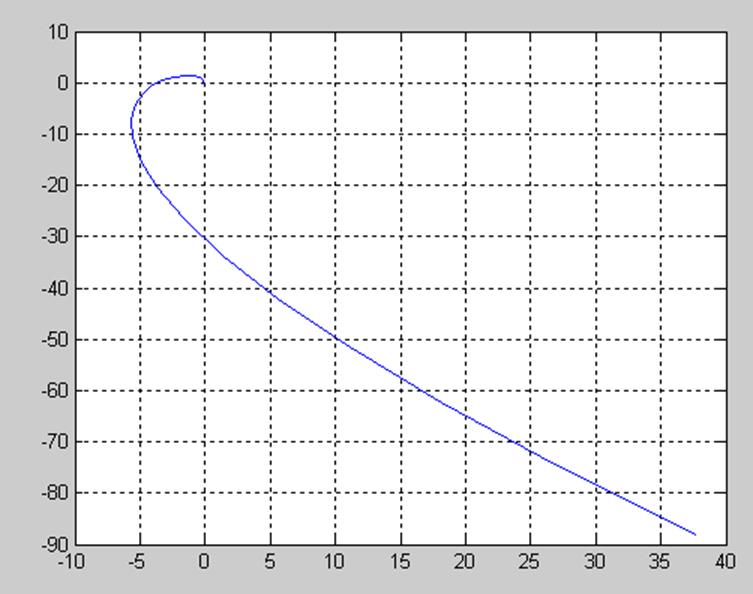
3.3.2 Построение временных переходных характеристик.
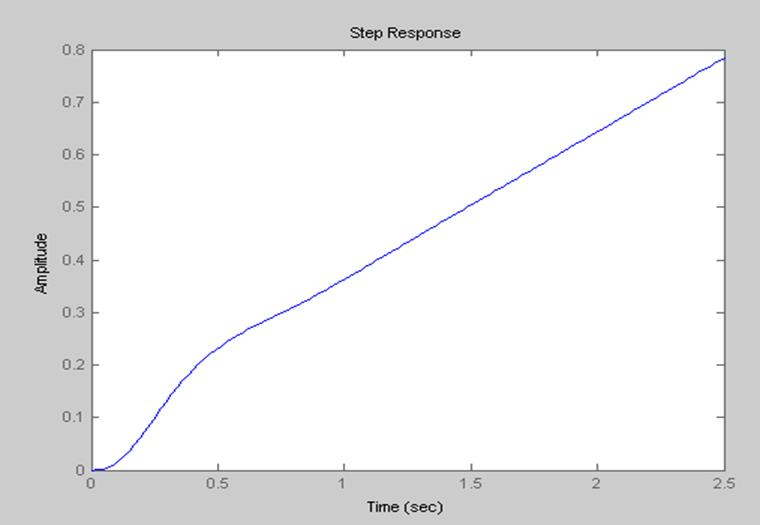
Непрерывная временная характеристика.
Импульсная переходная характеристика.
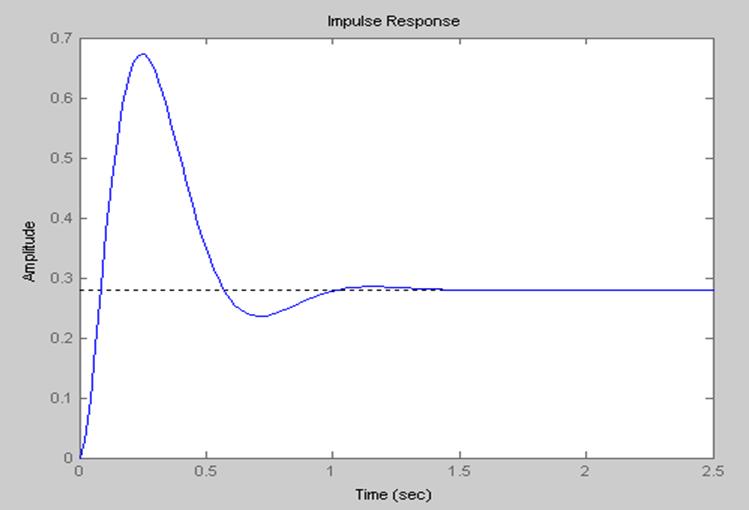
Система находиться на грани устойчивости, т.к. график проходит через начало координат, пересекает последовательно 4 квадранта и проходит против часовой стрелки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.