Министерство образования и науки
Московский государственный университет леса
Кафедра УАП ЛПК

Лабораторная работа № 6 по ТАУ:
Определение устойчивости по критерию Найквиста, Гурвица, Раусса и по логарифмическим частотным характеристикам.
Выполнил: студент группы АП-31
Морозов А. Е.
Проверил: Дорошенко В. А.
Москва 2010
Содержание:
1. Исходные данные.
2. Определение устойчивости по критерию Найквиста.
3. Определение устойчивости по критерию Гурвица.
4. Определение устойчивости по критерию Раусса.
5. Определение устойчивости по логарифмическим частотным характеристикам.
6. Временные переходные характеристики.
1. Исходные данные:
1. Передаточная функция замкнутой системы регулирования без корректирующего звена:
Wz=
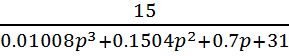
2. Передаточная функция корректирующего звена:
W=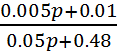
3. Передаточная функция замкнутого звена с учетом корректирующего звена:
Wz=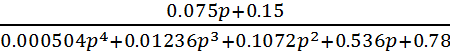
4. Передаточная функция разомкнутой системы регулирования без корректирующего звена:
Wr=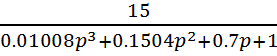
5. Передаточная функция разомкнутой системы регулирования с учетом корректирующего звена:
Wr=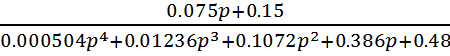
2. Определение устойчивости по критерию Найквиста.
2.1. Определение устойчивости САР без корректирующего звена.
Wr=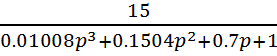
D=![]()
>> P=[0.01008 0.1504 0.7 1];
>> roots(P)
ans = -7.1429 -5.0000 -2.7778
Корни характеристического полинома разомкнутой передаточной функции являются отрицательными, поэтому рассматриваем 1 случай критерия Найквиста.
num=[0 15];
den=[0.01008 0.1504 0.7 1];
nyquist(num,den)
Система неустойчива, т.к. АФЧХ охватывает точку (-1, j0).
2.2. Определение устойчивости САР с учетом корректирующего звена.
Wr=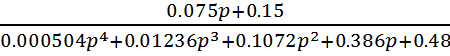
D=![]()
>> P=[0.000504 0.01236 0.1072 0.386 0.48];
>> roots(P)
ans = -9.6173 -7.1279 -5.0000 -2.7786
Корни характеристического полинома разомкнутой передаточной функции являются отрицательными, поэтому рассматриваем 1 случай критерия Найквиста.
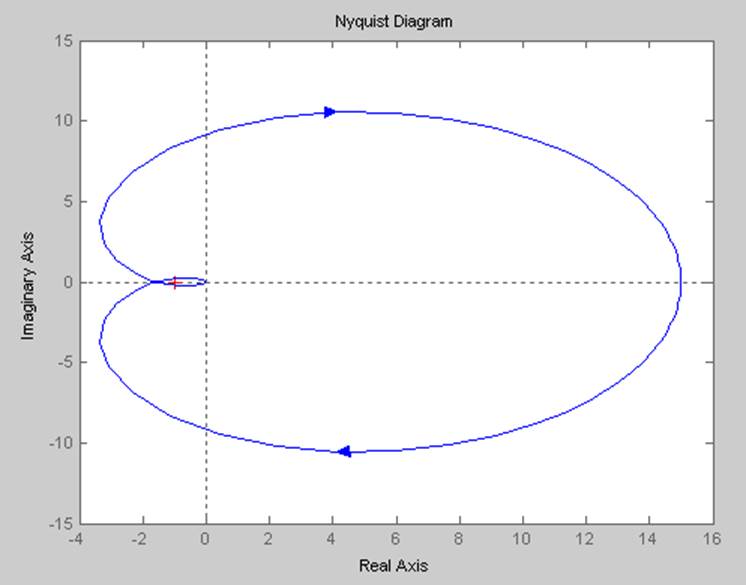
num=[0.075 0.15];
den=[0.000504 0.01236 0.1072 0.386 0.48];
nyquist(num,den)
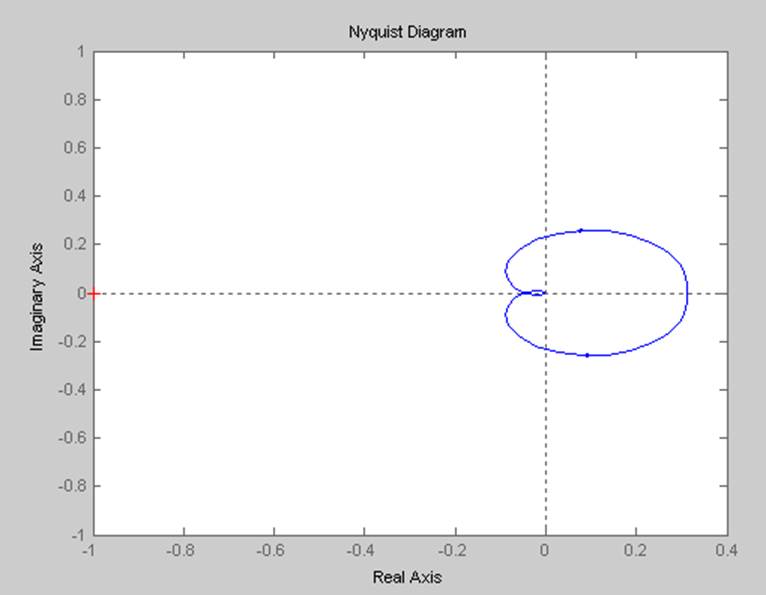
Система неустойчива, т.к. АФЧХ не охватывает точку (-1, j0).
2.3. Определение устойчивости САР с учетом корректирующего звена без свободного члена.
Wr=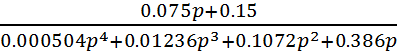
D=![]()
>> P=[0.000504 0.01236 0.1072 0.386 0];
>> roots(P)
ans = 0 -12.2845 -6.1197 + 4.9894i -6.1197 - 4.9894i
Корни характеристического полинома разомкнутой передаточной функции имеет нулевой корень, поэтому рассматриваем 2 случай критерия Найквиста.
num=[0.075 0.15];
den=[0.000504 0.01236 0.1072 0.386 0];
nyquist(num,den)
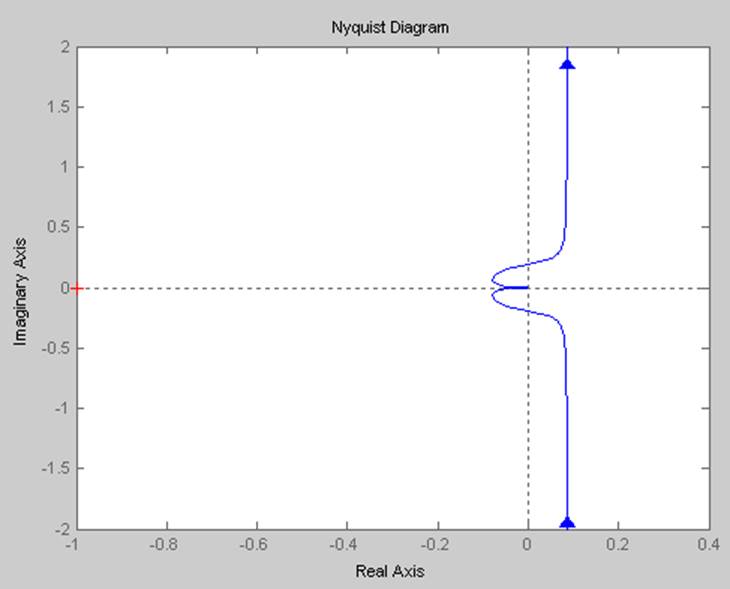
3. Определение устойчивости по критерию Гурвица.
3.1. Определение устойчивости САР без корректирующего звена.
Wz=
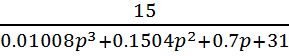
P=![]()
Г=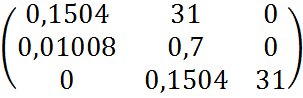
1. Все коэффициенты больше 0.
2. ![]() 0.7*0.1504-31*0.01008=-0.2072
0.7*0.1504-31*0.01008=-0.2072
Система неустойчива,
т.к. определитель ![]() меньше 0.
меньше 0.
3.2. Определение устойчивости САР с учетом корректирующего звена.
Wz=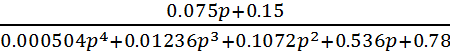
Р=![]()
Г=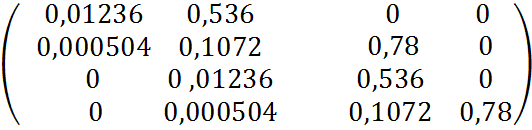
1. Все коэффициенты больше 0.
2. ![]() 0.00044
0.00044
Система устойчива, т.к.
все коэффициенты больше 0 и определитель ![]() больше 0.
больше 0.
3.3. Определение устойчивости САР с учетом корректирующего звена без свободного члена.
Wz=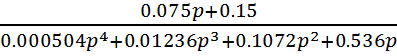
Р=![]()
Г=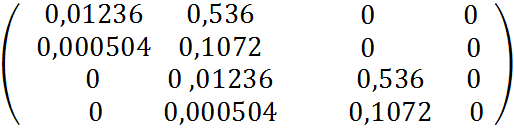
1. Все коэффициенты больше 0.
2. ![]() 0,0005628
0,0005628
4. Определение устойчивости по критерию Раусса.
4.1. Определение устойчивости САР без корректирующего звена.
Wz=
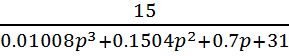
P=![]()
|
31 |
0,1504 |
|
0,7 |
0,01008 |
|
-0,296 |
- |
|
- |
- |
Система неустойчива, т.к. не все элементы 1-ого столбца положительны.
4.2. Определение устойчивости САР с учетом корректирующего звена.
Wz=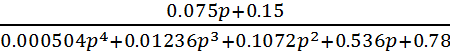
Р=![]()
|
0,78 |
0,1072 |
0,000504 |
|
0,536 |
0,01236 |
0 |
|
0,089 |
0,000504 |
0 |
|
0,0093 |
0 |
- |
|
0,00504 |
- |
- |
Система устойчива, т.к. все элементы 1-ого столбца положительны.
4.3. Определение устойчивости САР с учетом корректирующего звена без свободного члена.
Wz=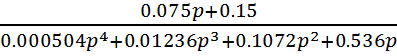
Р=![]()
|
0 |
0,1072 |
0,000504 |
|
0,536 |
0,01236 |
0 |
|
0,1072 |
0,000504 |
- |
|
- |
- |
- |
|
- |
- |
- |
Система находится на границе устойчивости, т.к. в 1-ом столбце содержится элемент равный 0.
5. Определение устойчивости по логарифмическим частотным характеристикам.
5.1. Определение устойчивости САР без корректирующего звена.
Wr=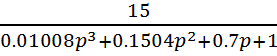
>> bode(Wr)
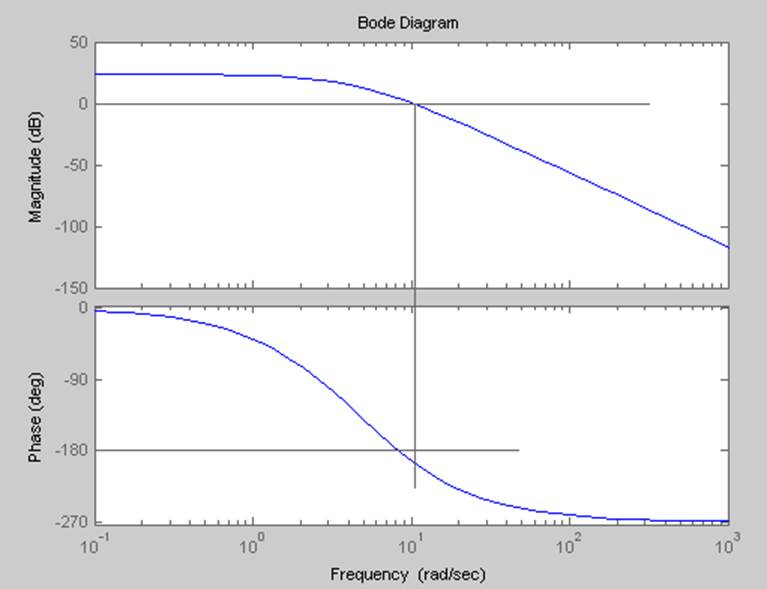
Система неустойчива,
т.к. ЛФЧХ пересекает уровень 18![]() до частоты перехода.
до частоты перехода.
5.2. Определение устойчивости САР с учетом корректирующего звена.
Wr=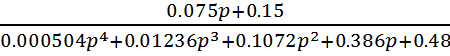
bode(Wr)
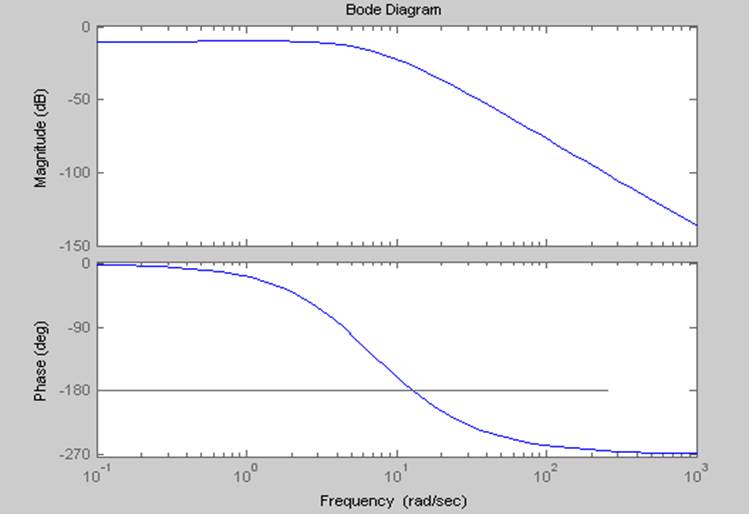
5.3. Определение устойчивости САР с учетом корректирующего звена без свободного члена.
Wr=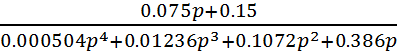
bode(Wr)
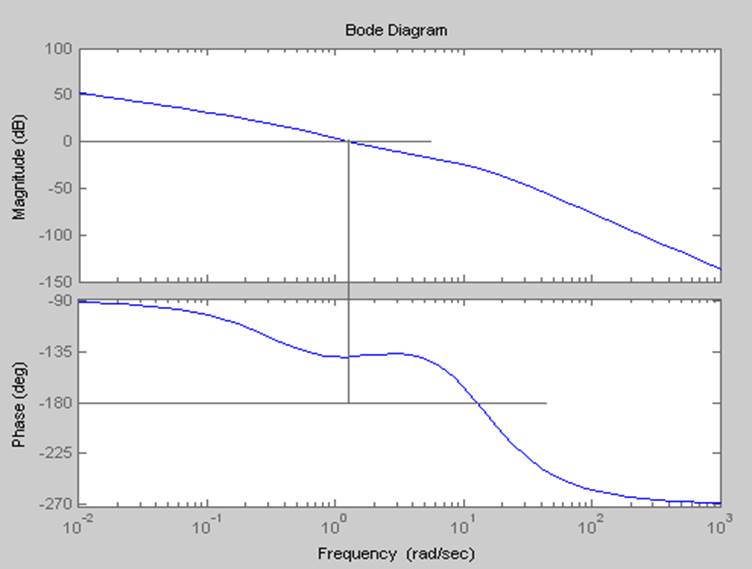
6. Временные переходные характеристики.
6.1. Передаточная функция замкнутой системы регулирования без корректирующего звена:
Wz=
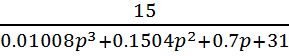
Непрерывная временная характеристика.
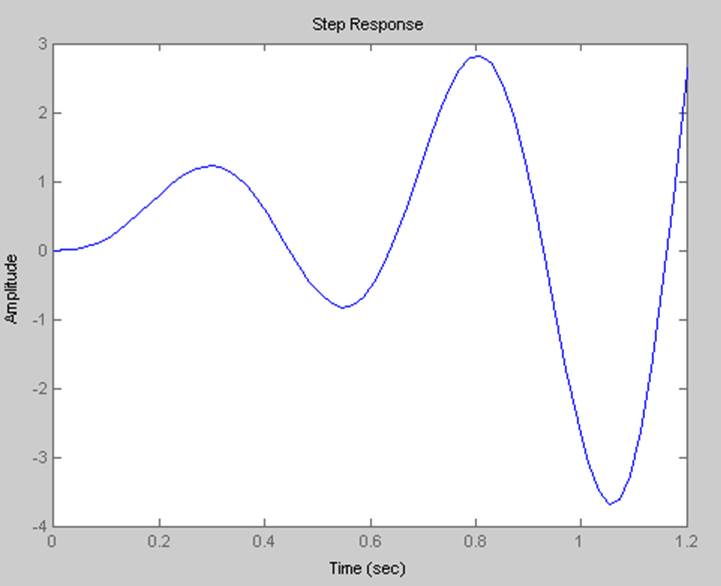
Импульсная характеристика.
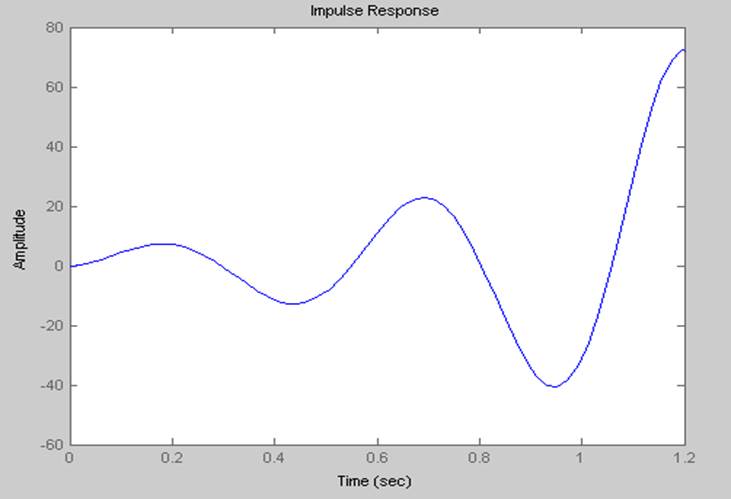
6.2. Передаточная функция замкнутого звена с учетом корректирующего звена:
Wz=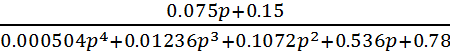
Непрерывная временная характеристика
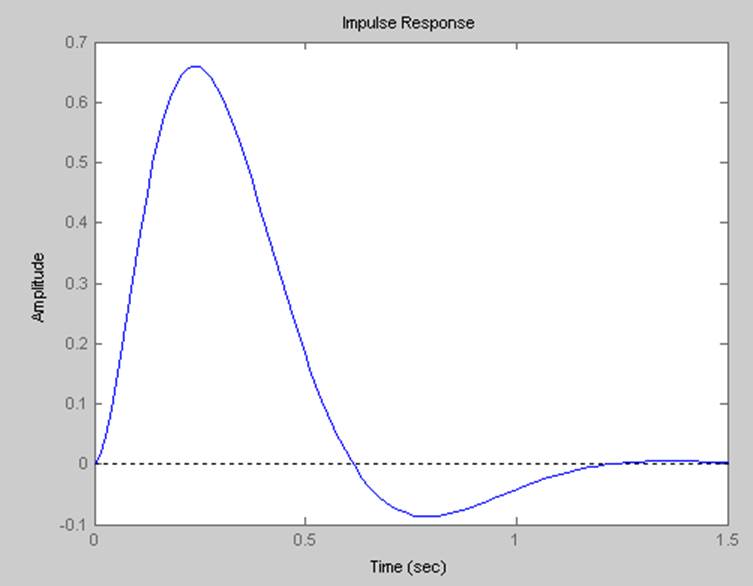
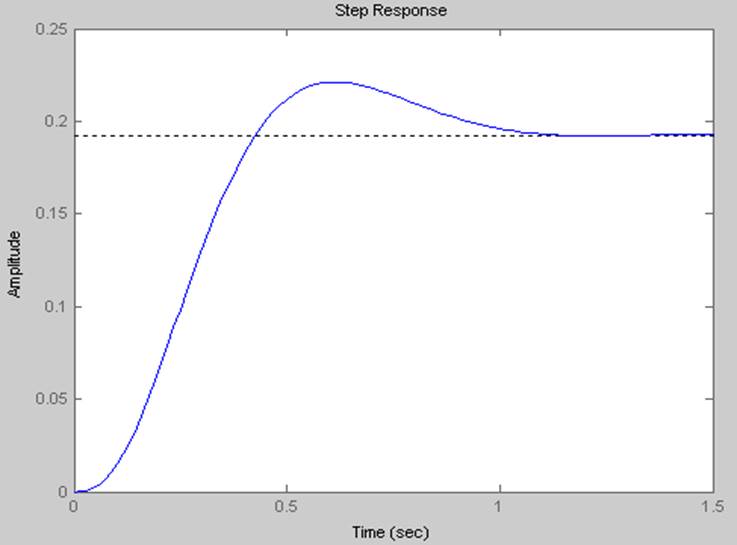 Импульсная
характеристика.
Импульсная
характеристика.
6.3. Передаточная функция замкнутого звена с учетом корректирующего звена без свободного члена:
Wz=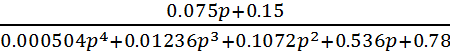
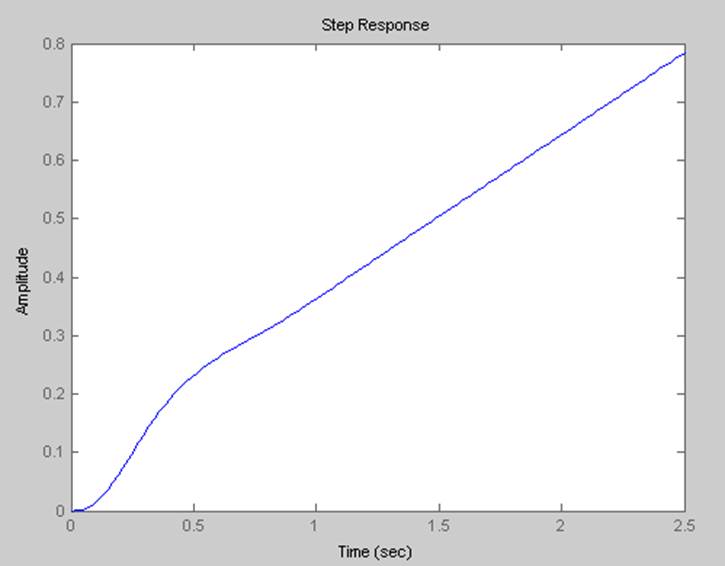
Непрерывная временная характеристика
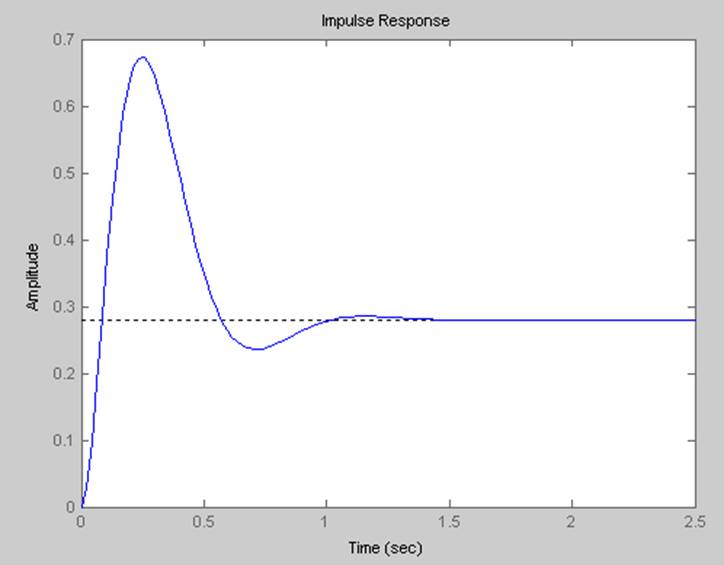
Импульсная характеристика.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.