Усиление железобетонных конструкций с изменением статической схемы, страница 5

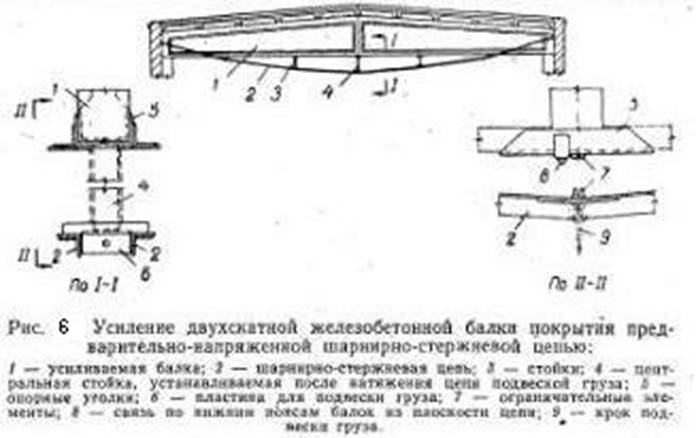
Усиление с использованием шпренгельных систем.

Шпренгель – это стержневая конструкция, в которой за счет совместных деформаций с усиливаемой железобетонной конструкцией возникает растягивающее усилие Р. Его горизонтальная проекция – распор N'=N–Т (где T – сила трения при перегибе стержней) создает положительный (загружающий) изгибающий момент М_о=N_хе, а вертикальные проекции D – отрицательный (разгружающий) момент М_p. Кроме того, в опорных участках возникают и разгружающие поперечные силы Q_p, в результате чего суммарные усилия ΣM и ΣQ оказываются меньшими, чем усилия М_q и Q_q от внешней нагрузки (рис.1).

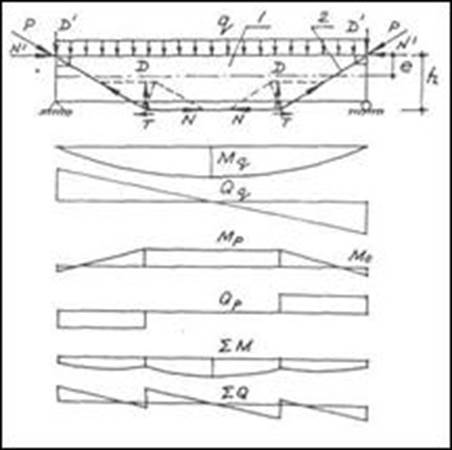
Рис.1. Усиление шпренгельными затяжками.

  Целесообразно, казалось бы, концы шпренгеля опустить до уровня нейтральной оси усиливаемой балки, исключить образование в ней М0 и повысить, тем самым, эффективность усиления. Однако ожидаемого результата это не даст, поскольку одновременно уменьшатся значения D. Можно передвинуть весь шпренгель книзу, тогда и значения D сохранятся и M0 поменяет знак с положительного на отрицательный. Но в этом случае существенно усложняется конструкция шпренгеля, а сам он уменьшает полезный объем здания, поэтому такое решение широкого применения не нашло (а в зданиях с кранами вообще исключено).
  В качестве шпренгельной затяжки используют стержневую арматурную сталь больших диаметров, а при необходимости – и прокатные профили из уголков или швеллеров. Как и в случае со стальными балками, эффективность работы шпренгелей без предварительного напряжения весьма невелика. Опыт проектирования показывает, что если шпренгели включить в работу даже с самого начала (т. е. установить их при полностью снятой полезной нагрузке), то разгрузить железобетонные балки они в состоянии на 5...20%.
  Требуемую величину распора N определяют из величины требуемого уменьшения изгибающих моментов и поперечных сил на величину соответственно М_p и Q_p . Далее необходимо найти, какая часть этого распора приходится на совместные деформации шпренгеля с балкой, а какая часть – на его преднапряжение. Точный расчет здесь довольно сложен, поскольку связан с поворотом торцов и линией прогибов балки, зависящих от схемы нагрузки, изгибной жесткости балки, осевой жесткости шпренгеля и др. факторов. Поэтому с достаточной для практики точностью пользуются приближенным расчетом:

,

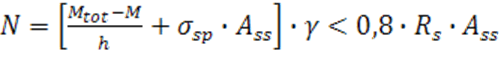где М_tot (на рис. 1 обозначен как М_q и М₁ – изгибающие моменты после и до усиления, h – стрела провеса шпренгеля (плечо между N и N'), σ_sp – величина преднапряжения шпренгеля, A_ss – площадь сечения стержней шпренгеля, γ= 0,8 – коэффициент, учитывающий потери напряжений от обмятия контактных поверхностей, 0,8 – коэффициент условий работы стали. Приравняв выше найденную величину распора к этому выражению, можно определить величину усилия предварительного натяжения, а из нее и площадь сечения стержней шпренгеля. Если усиление проводится при действии полной нагрузки на балку, то первое слагаемое в квадратных скобках становится равным нулю и все усилие N создается только за счет преднапряжения шпренгеля. Саму балку после усиления рассчитывают по прочности как внецентренно сжатый элемент на действие сжимающей силы N' (распора за вычетом потерь от трения при перегибе) и изгибающего момента ΣМ.

Усиление железобетонных, металлических и деревянных балочных конструкций при помощи шпренгельных затяжек из высокопрочных канатных и стержневых элементов с предварительным напряжением.

Использование предварительного напряжения позволяет не только усилить конструкцию, но и ликвидировать уже имеющиеся прогибы и трещины.

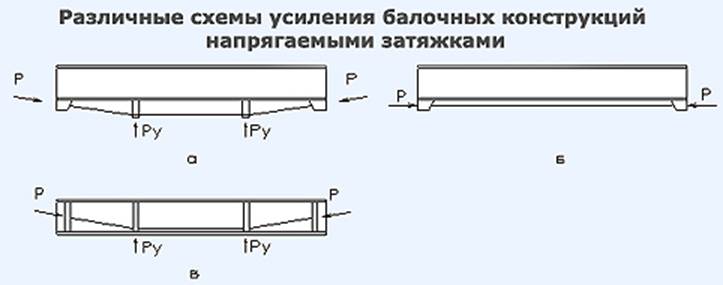
а). Шпренгелные затяжки с развитием сечения
б). Прямолинейные затяжки
в). Шпренгельные затяжки без развития сечения
Устройство шпренгельных преднапрягаемых затяжек позволяет переносить нагрузку из пролета непосредственно на опору, тем самым разгружая конструкцию.

Литература:

1.  http://www.beton-karkas.ru

2.  Хило Е.Р., Попович Б.С. ;Усиление железобетонных конструкций с изменением расчетной схемы и напряженного состояния. –Львов: «Высшая школа», 1976.-147 с.