Расчет переходных процессов импульсных САУ. Применение ЛЧХ для импульсных САУ

21. РАСЧЕТ ПЕРЕХОДНЫХ  ПРОЦЕССОВ  ИМПУЛЬСНЫХ  САУ

Пусть имеем структурную схему замкнутой импульсной САУ (рис.21.1).

 

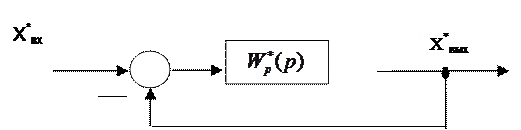Рис. 21.1

Найдем передаточную функцию замкнутой системы и изображение выходной величины

              

Для перехода от изображения к оригиналу существуют методы:

1. Для перехода от изображения  к дискретным значениям выходного сигнала x_вых(lT) можно воспользоваться формулой обратного преобразования Лапласа для дискретных сигналов:

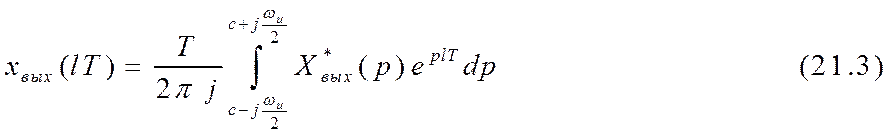            2. Если изображение выходного сигнала имеет вид дробно-рациональной функции от e^pT, например, 

,

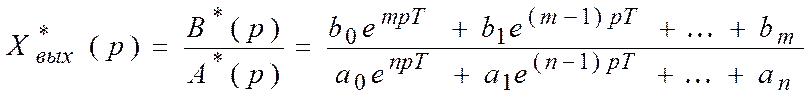тогда дискретные значения выходного сигнала можно найти по формуле разложения

где: p_k – корни характеристического уравнения A*(p)=0,

 .  .
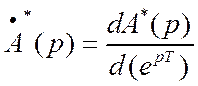В частном случае, если известна передаточная функция системы,

,

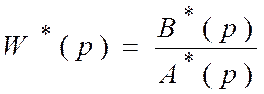то можно найти реакцию на типовые входные сигналы, то есть  весовую и переходную функции.

Дискретные значения переходной функции равны 

.

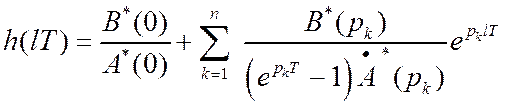Дискретные значения функции веса можно определить

  .

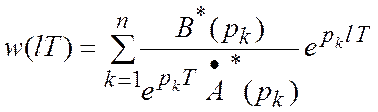3. Если входной сигнал имеет произвольную форму, то, зная весовую функцию системы, можно найти дискретные значения сигнала на выходе системы при произвольном воздействии на ее входе.

                                               

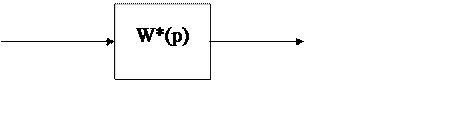
                                      Х*_вх                                                Х*_вых

 

Рис. 21.2

,

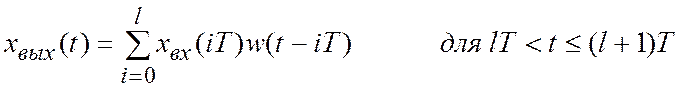где w(t) – весовая функция замкнутой системы.

Для t = lT, то есть дискретных моментов, получим

.

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                    

       

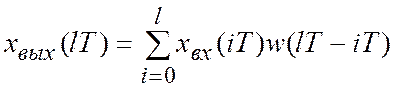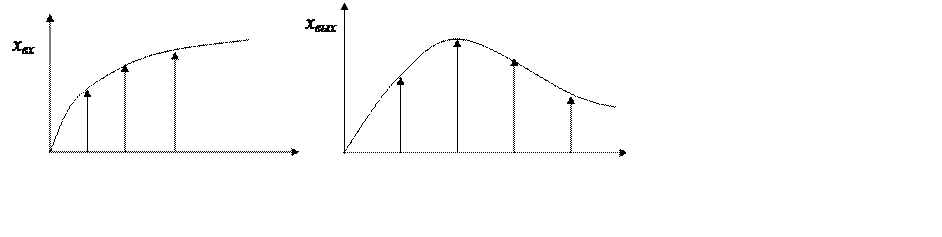
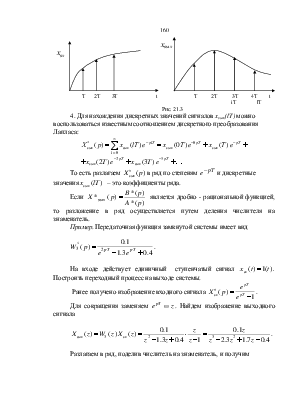
        T      2T        3T                           t                          T         2T           3T               4T        t                                                                                                                    iT              lT

Рис. 21.3

4. Для нахождения дискретных значений сигналов x_вых(lT) можно воспользоваться известным соотношением дискретного преобразования

Лапласа:

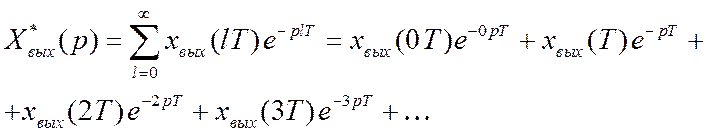
То есть разлагаем в ряд по степеням  и дискретные значения  – это коэффициенты ряда.

Если 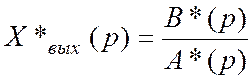  является дробно - рациональной функцией, то разложение в ряд осуществляется путем деления числителя на знаменатель.

Пример. Передаточная функция замкнутой системы имеет вид

.

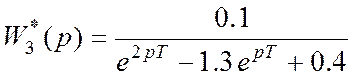На входе действует единичный  ступенчатый сигнал . Построить переходный процесс на выходе системы.

 Ранее получено изображение входного сигнала .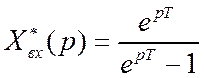

Для сокращения заменяем . Найдем изображение выходного сигнала

.

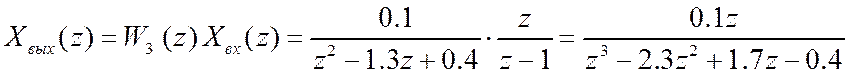Разлагаем в ряд, поделив числитель на знаменатель, и получим

X_вых(z) = 0.1 z^-2+0.23 z^-3+0.36 z^-4  + …

Коэффициенты при z ^-1 = e^-pT у частного представляет собой значения дискретной выходной величины . Таким образом,  получим:

при l = 0 и l = 1 имеем x_вых(0) = x_вых(T) = 0, далее получаем x_вых(2T) = 0.1,  x_вых(3T) = 0.23, x_вых(4T) = 0.36 и так далее.

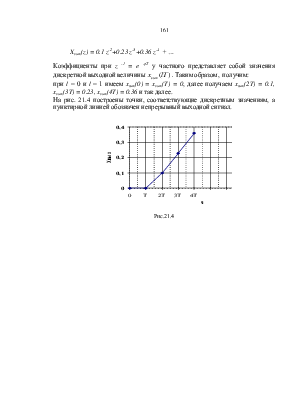
На рис. 21.4 построены точки, соответствующие дискретным значениям, а пунктирной линией обозначен непрерывный выходной сигнал.

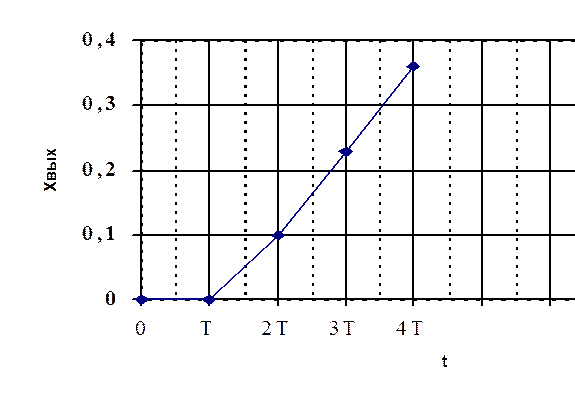
Рис.21.4

22. ПРИМЕНЕНИЕ ЛЧХ ДЛЯ ИМПУЛЬСНЫХ САУ

22.1. ЛЧХ импульсных САУ

ЛЧХ для непрерывных САУ позволили развить приближенные методы, упрощающие решение задач анализа и синтеза САУ.

Целесообразно использовать ЛЧХ и для импульсных систем, когда не только расчет частотных характеристик, но даже получение передаточных функций затруднено.

Однако простое применение логарифмических масштабов для частотных характеристик импульсных САУ не дает преимуществ, так как передаточные функции имеют трансцендентный характер.

Однако частотные характеристики можно построить, если использовать замену переменных: