Для одномерных элементов пространства объем образуется умножением длины на площадь поперечного сечения т. е. интегрирование по длине.
В этом случае Якобиан имеет вид:
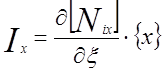 ;
;
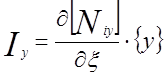 ;
;
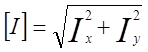 - длина элемента;
- длина элемента;
Вектор нагрузок образующийся в следствии начальной деформации можно определить по соотношению вида:
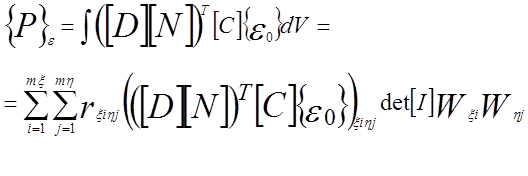 ;
;
где ![]() ,
,![]() -
весовые коэффициенты;
-
весовые коэффициенты;
![]() -
радиус точки интегрирования;
-
радиус точки интегрирования;
Вектор поверхностных нагрузок определяется по формуле:
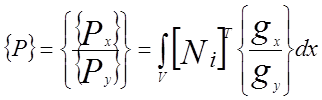 .
.
Вектор
нагрузок обусловленный температурой среды ![]() и
коэффициентом теплообмена
и
коэффициентом теплообмена ![]() на поверхности
на поверхности ![]() имеет вид:
имеет вид:
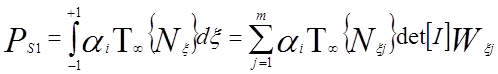 ;
;
РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
В ЗАДАЧЕ ТЕПЛОПРОВОДНОСТИ
В настоящее время одним из самых распространенных и, пожалуй, наиболее мощным численным методом в механике деформируемого твердого тела является метод конечных элементов. В том числе он с успехом может быть применен и для решения задач нестационарной теплопроводности. В случае, если термомеханические и геометрические характеристики и нагрузки имеют резкие изменения (например, "скачки" в толщинах или разрывные температурно-силовые нагрузки), то метод конечных элементов, пожалуй, единственный из других численных методов позволяет получить решение в рамках единой расчетной схемы. Метод объединяет в себе достоинства дискретных методов по степени передачи изменяющихся характеристик конструкции и континуальных вариационных методов по наглядности математического подхода, по простоте получения решения и удобству выполнения различных комбинаций граничных условий.
Кратко идея метода конечных элементов в форме метода перемещений (или когда за неизвестную функцию принята температура) выглядит так. Объем, занимаемый конструкцией, разбивается на довольно большое число элементарных объемов, называемых конечными элементами. Степень густоты сетки зависит от степени изменения решения задачи. Линии, по которым стыкуются конечные элементы, называются узловыми линиями, а места, где сходится несколько узловых линий - узловыми точками. Предполагается, что перемещения или температурное поле всей конструкции могут быть с достаточной точностью представлены перемещениями или температурами узловых точек. Вводятся функции формы, аппроксимирующие перемещения (температуры) внутри каждого конечного элемента через перемещения (температуры) узловых точек.
ДИСКРЕТНАЯ МОДЕЛЬ
Изложим вывод основных соотношений метода конечных элементов в задаче теплопроводности, базирующийся на вариационном подходе. Для построения дискретного аналога функционала определим температурное поле внутри каждого элемента таким образом, чтобы оно было непрерывным на границе двух смежных элементов и единственным образом выражалось через температуры узловых точек.
Пусть температура внутри т-го конечного элемента аппроксимируется матричным уравнением
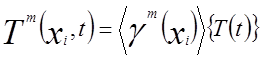 , (1)
, (1)
где ![]() —
вектор-столбец узловых температур для полной системы конечных элементов;
—
вектор-столбец узловых температур для полной системы конечных элементов;
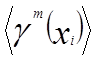 - вектор-строка
коэффициентов, зависящих от пространственных координат
- вектор-строка
коэффициентов, зависящих от пространственных координат ![]() ,
соответствующих координатам x,y,z.
,
соответствующих координатам x,y,z.
Большинство коэффициентов в 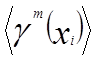 равно
нулю, так как тепловое состояние подобласти полностью определяется
температурой узлов рассматриваемого конечного элемента или соседних с ним
элементов.
равно
нулю, так как тепловое состояние подобласти полностью определяется
температурой узлов рассматриваемого конечного элемента или соседних с ним
элементов.
Дифференцируя уравнение (1) по пространственным координатам, получаем выражение вектора температурного градиента
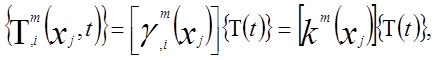 (2)
(2)
где индекс после запятой означает дифференцирование по координате, а квадратными скобками обозначена прямоугольная матрица.
Аналогичным образом определяется температура границы
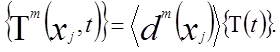 (3)
(3)
Запишем функционал в виде суммы по всем элементам системы
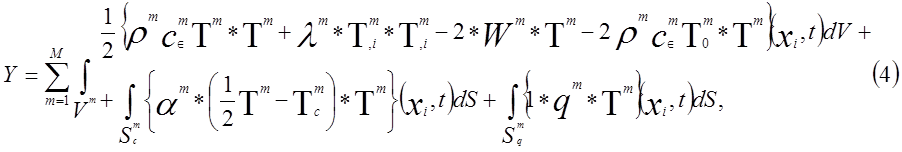 где М — общее число конечных элементов.
где М — общее число конечных элементов.
Дискретный аналог функционала
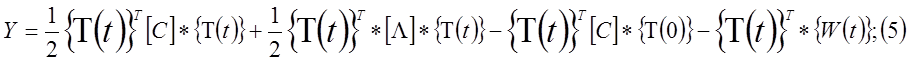
где 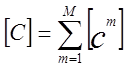 -матрица теплоемкости;
-матрица теплоемкости;
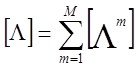 -матрица теплопроводности;
-матрица теплопроводности;
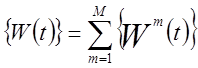 -вектор-столбец тепловых сил;
-вектор-столбец тепловых сил;
Элементарные матрицы ![]() имеет вид
имеет вид
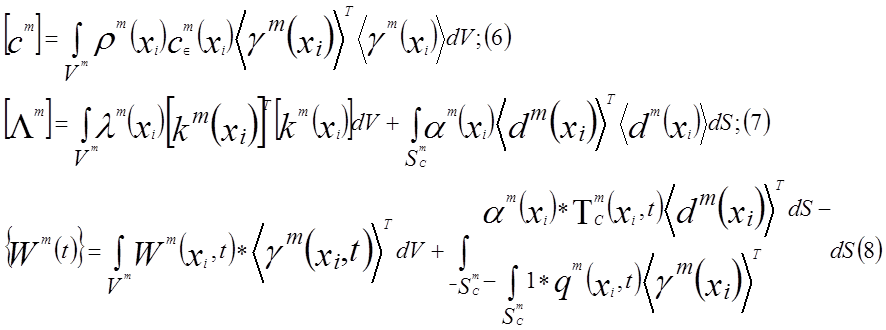
Дифференцируя квадратичную функцию многих переменных по каждой из узловых температур, получаем матричное уравнение
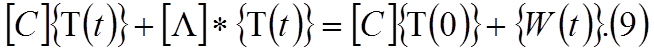
СПИСОК ЛИТЕРАТУРЫ:
С.–Петербург 1996 год 2 тома.
3. Текст лекций.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.