Механика \ Механика деформируемого твердого тела

Вычисление собственных значений cобственных векторов действительной симметричной матрицы, страница 2

где все невыписанные элементы — нулевые.

Аналогично матрица L строится как предел последовательности матриц Аkудовлетворяющих соотношению

    (k=1,2,…. ),

где  A0=A.

При преобразовании матрицы Аk-1с помощью матрицы простого поворота на каждом шаге аннулируется внедиагональный элемент    (lm)

Из условия , где — элемент преобразованной матрицы, получаем соотношение

Tg2θ=, 

где qвсегда выбираем в пределах [2q]π/2

При таком выборе qимеем:

sinq= 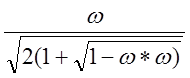;                 cosθ=;

где

ω=sign.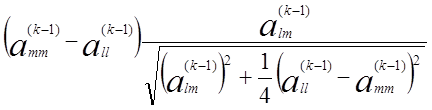

Матрица Ak-1 преобразуется по формулам:

         (i,j l,m);

      (il,m);

;

;

;

;

Внедиагональные элементы аннулируются циклически в соответствии со следующей нумерацией пар ( l,m) :

(1,2) , (1,3) , (2,3) , (1,4) , (2,4) , (3,4) . . . , (1, N) , (2, N) , . . . , (N-1, N) .

Для того чтобы не аннулировать малые внедиагональные элементы, в то время как еще присутствуют большие по значению элементы, осуществляется проверка условия:

││<V/N,

где Vвначале выбирается равной V0=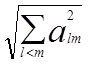, а после того, как все внедиагональные элементы станут по модулю меньше, чем V0,происходит уменьшение этой величины в N раз.

Указанный процесс продолжается до тех пор, пока все внедиагональные элементы не станут меньше по модулю, чем величина

V1=10-6V0/N.

Матрица R, содержащая собственные векторы матрицы А, вычисляется как произведение матриц простых поворотов Tk  (k = 1,2,...).

Обращение к подпрограммам имеет соответственно вид:

CALL EIGEN (A,R,N,MV);

CALL DEIGEN (A,R,N,MV);

А — массив, содержащий верхнюю треугольную часть исходной симметричной матрицы (точность обычная или удвоенная). При выходе из подпрограммы элементы этого массива, соответствующие диагональным элементам матрицы, содержат соб­ственные значения, расположенные в порядке убывания;

R — массив,  содержащий  при выходе из подпрограммы  матрицу собственных векторов, расположенную по столбцам в той же последовательности, что и собственные значения (точность обычная или удвоенная);

N — порядок матриц Aи R;

MV— параметр, определяющий характер вычислений;

МV = 0 — вычисляются собственные значения и собственные векторы;

МV = 1 — вычисляются только собственные значения (массив R в этом случае не используется, но имя его должно быть обязательно задано в обращении).

Особенности формирования вектора нагрузок применительно

к тепловой задаче

Тепловой баланс тепла в произвольный момент времени с учетом аппроксимации его объема и теплофизических параметров, описывается системой обыкновенных диффиренцированных уравнений первого порядка.

Пусть на границе поверхности S1 происходит конвективный теплообмен интенсивностью

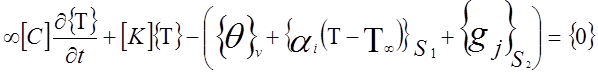
   при   на S3

где       [C] – матрица теплоемкости;

            [K] – матрица теплопроводности;

{θ}v – вектор столбец нагрузок, вызванный внутренним теплоисточником в объеме V;

{gi}S1 – вектор теплопотока на S2;

 - вектор теплоотдачи на S1;

При рассмотрении задачи нестационарной теплопроводности, каждый элемент объема тела VK обладает конкретными теплофизическими свойствами:

            - теплопроводность λК [Вт/см3.градус];

            - теплоемкость Сρk [Дж/см.3градус];

- внутренние потоки QK [Вт/см3.];

На поверхности S1 происходит конвективный теплообмен интенсивностью  

Где      - коэффициент теплоотдачи температуры стенки [Вт/см3.градус];

      - температура среды, омывающей поверхность [градус];

       Т – температура стенки тела;

            На поверхности S1 действуют теплопотоки  [Вт/см.2], приводящие к изменению температуры в объеме тела, a на отдельных участках поверхности тела S3 температура задана и характер изменения ее во времени известен.

            Выбранная дискретизация исследуемого объема среды при рассмотрении различных физических задач остается в основном неизменным, что говорит о ее универсальности. Индексация объемов и поверхностей показанная здесь одинаковым обозначением на самом деле не совпадает при решение различных задач. Это обусловлено тем, что физические процессы как например, охлаждение за счет теплоотвода и нагружение от сосредоточенных сил, происходит в разных областях данного тела.

            Для того чтобы правильно решать уравнение необходимо выполнить некоторые условия:

-  необходимо в матрице теплопроводности, полученной для объема, добавить матрицу теплопроводности, полученную в следствии дополнительного теплообмена на поверхности S1 c коэффициентом .

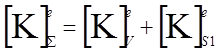                       для одного элемента.                       

Скачать файл