Осесимметричные задачи концентрации напряжений в элементах авиационных конструкций

Мавлютов Р.Р. Концентрация напряжений в элементах авиационных конструкций. ¾М.: Наука, 1981. 141с.

4. ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ

В ЭЛЕМЕНТАХ АВИАЦИОННЫХ КОНСТРУКЦИЙ

       4.1. Концентрация напряжений в стержнях с выточками и галтелями

К числу типичных элементов конструкций, которые могут быть рассчитаны в осесимметричной постановке, можно прежде всего отнести валы, имеющие выточки и галтели, резьбовые соедине­ния хвостовиков сопловых лопаток, стяжные болты роторов комп­рессоров, фланцевые соединения корпусных деталей, болтовые и шпилечные соединения корпусов и др.

В настоящем параграфе приведены результаты исследований стержней с выточками и галтелями на основе численного решения задач упругости, пластичности и ползучести методом конечного элемента. Рассмотрены случаи простого и сложного нагружения.

С целью получения сравнительных данных сначала произведен расчет распределения напряжений в стержнях, работающих при упругих деформациях. Рассмотрены стержни, имеющие диаметр 010 мм, угол раствора выточки 60°, различные радиусы впа­дины и глубины iот 0,5 до 4мм. Стержни выполнены из материала ЭИ437Б (от = 56 кгс/мм²).

Исследовано влияние конфигурации выточки на ее напряжен­ное и деформированное состояния. На рис. 4.1 пунктирными ли­ниями изображены в качестве примера типичные эпюры напря­жений, построенные по результатам расчета стержня, имеющего радиус выточки г = 0,15 мм. На графиках (рис. 4.2 и 4.3) пока­заны зависимости коэффициентов концентрации напряжений и де­формаций от отношения радиуса к глубине выточки (r/f) и угла раствора выточки (а).

Анализ показывает, что наиболее существенное влияние на уровень напряженности стержня оказывают радиус и глубина выточки, причем с увеличением радиуса и уменьшением глубины величины k_aи k_&уменьшаются особенно значительно при неболь­ших отношениях г/1 (до значений порядка 0,2). Угол раствора вы­точки влияет незначительно (см. рис. 4.3, кривая 6). На этих же рисунках кривые 1—5 относятся к выточкам с глубинами 0,5; 0,915; 2; 3; 4 мм соответственно.

Выполнено сравнение с точным решением, полученным Г. Ней-бером [114] (см. рис. 4.3, пунктирные кривые). Установлено, что отличие в результатах незначительно.

109

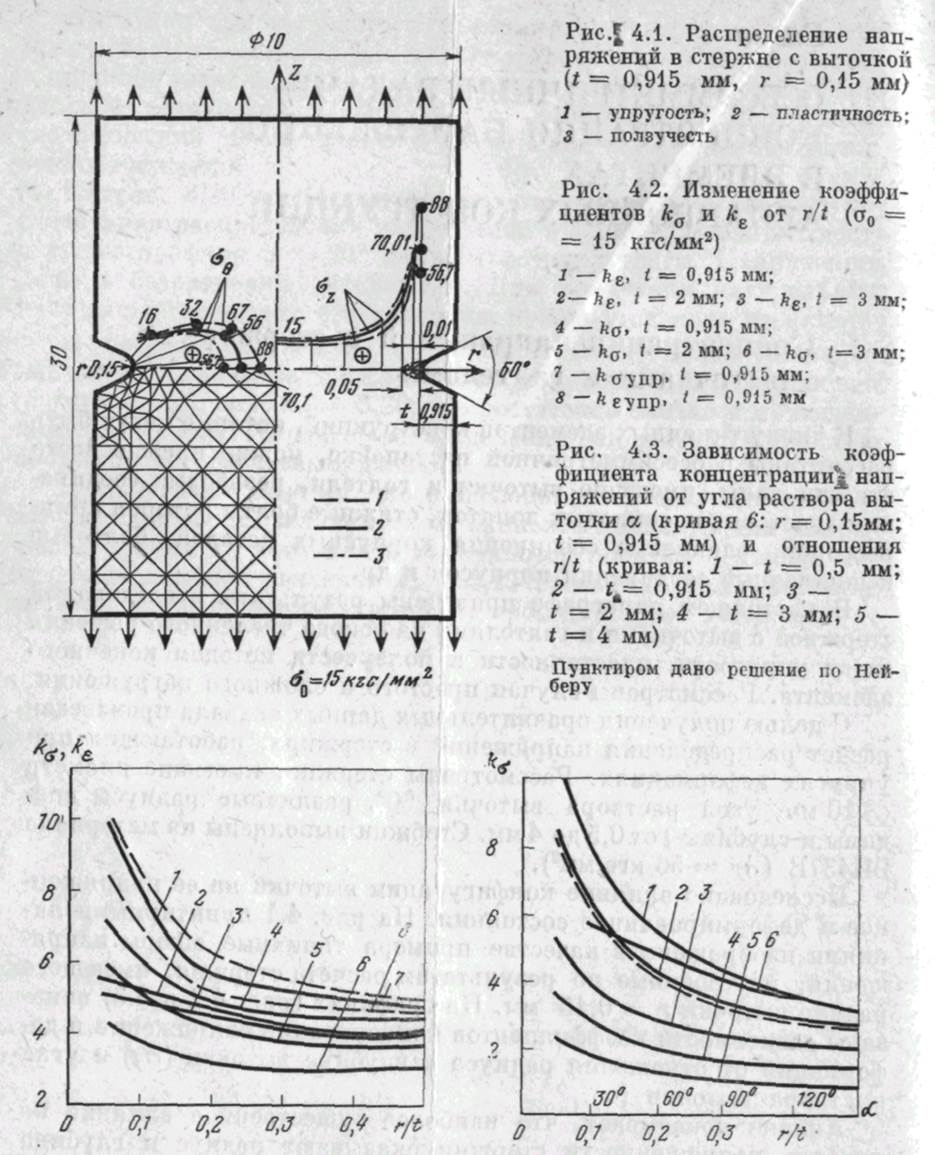
Pnc.J4.1. Распределение вац-ряжений в стержне с выточкой (t = 0,915 ыи, г = 0,15 мы)

1 — упругость; 2 — пластичность; з — ползучесть

Рис. 4.2. Изменение коэффи­циентов k_aи fc_£ от r/t(0₀ = = 15 кгс/мм²) (1 — *— fc_e, 1

* — fco.  '— h_a, t 1 — k » —h оупр гупр- •• 0,915 мм; 2 мм; з — ft_e, ( 0,915 mm;

2 мм; О — h₀,

I «= 0,915 mm;

I = 0,915 mm

Зны;

Рис. 4.3. Зависимость коэф­фициента концентрации^ нап­ряжении от угла раствора вы-точки а (кривая 6: г = 0,15мм; t= 0,915 мм) и отношения r/t(кривая: 1 — t = 0,5 мм; 2 — «.= 0,915 ым; 3 — t= 2 мм; 4 — t= 3 мм; 5 — t = 4 мм)

Пунктиром дано решение по Нейберу

0,3       0,4    r/t

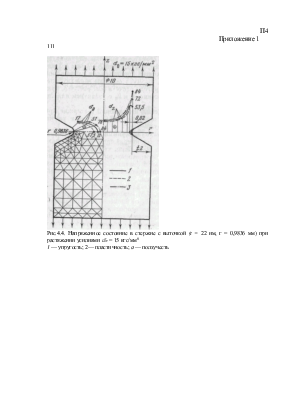
Изучено распределение напряжений в стержне при упруго¾пластических деформациях. В качестве примера на рис 4 4 сплошными линиями показаны эпюры распределения напряжений в стержнях, растянутых усилиями <т₀ = 15 кгс/мм². Зоны пласти­ческих деформаций заштрихованы. Анализ показывает, что как в пластинах с отверстием, в данном случае происходит некоторое смещение максимума нормальных напряжений в глубь стержня и выравнивание их по сечению.

110

Выполнена оценка влияния геометрии выточки на характер распределения и уровень напряжений. Кривые 1—б рис. 4.2 ил­люстрируют изменение коэффициентов концентрации напряжений и деформаций от отношения r/t, радиуса выточки к ее глубине. Сравнение их с результатами упругого расчета (см. рис. 4.2, кри­вые 7, 8) выявляет заметное снижение /с_ст и /с_г с развитием пласти­ческих деформаций.

Произведен расчет распределения напряжений в стержне при нагрузке <т₀ = 15 кгс/мм² и температуре 700° С с учетом разви­вающихся деформаций ползучести.

На рис. 4.4 для примера штрихпунктирными линиями показаны эпюры нормальных и контурных напряжений при выдержке стержня под нагрузкой в течение 80 ч. Ясно, что развитие дефор­маций ползучести приводит к перераспределению напряжений в исследуемых стержнях. При этом значительно (почти в 5 раз) возрастает зона пластических деформаций. Уровень максималь­ных напряжений заметно снижается.

В результате расчета стержней с различной геометрией выто­чек построены зависимости (рис. 4.5) коэффициентов концентра ции напряжений k_aи деформаций k_eот времени, показывающие, что влияние деформаций ползучести особенно заметно в первые 40 ч работы конструкции. В дальнейшем значения k_aи /с_е стаби­лизируются, что связано с выравниванием напряжений в рассмат­риваемых сечениях.

Представляет интерес сравнение результатов расчетов стерж­ней, один из которых однократно нагружался усилиями ст₀ = = 15 кгс/мм² (простое нагружение), другой — выдерживался под нагрузкой <to = 15 кгс/мм² в течение 80 ч, затем разгружался и вновь нагружался таким же усилием (сложное нагружение).

На рис. 4.6 показаны эпюры распределения напряжений для второго стержня. Сравнение их с результатами расчета первого стержня (рис. 4.6, пунктирные кривые) показывает существенное различие в напряженных и деформированных состояниях. В част­ности, во втором стержне уровень напряжений значительно мень­ше, а пластические деформации гораздо больше. Кроме того, ко­эффициент концентрации напряжений для второго стержня за­метно ниже (0,85 против 1,8), а коэффициент концентрации де­формаций выше и достигает величины 2,97.