Осесимметричные задачи концентрации напряжений в элементах авиационных конструкций, страница 2

Последний пример, относящийся к сравнению простого и слож­ного нагружений стержня, наглядно показывает, что «история» нагружения (в рассматриваемом примере повторность нагружения и время) оказывает существенное влияние на распределение нап­ряжений и должна быть учтена в уточненных расчетах стержней.

Изучено распределение напряжений в галтели цилиндрическо­го стержня из материала ЭИ-437Б в стадии упругости, пластич­ности и ползучести. Основные размеры стержня и результаты ра­счета его (радиус г = 0,3 мм) при растягивающих напряжениях <т₀ = 30 кгс/мм^а и о*о — 40 кгс/мм² показаны на рис. 4.7. Пунк­тирными линиями отмечены эпюры распределения напряжений

111

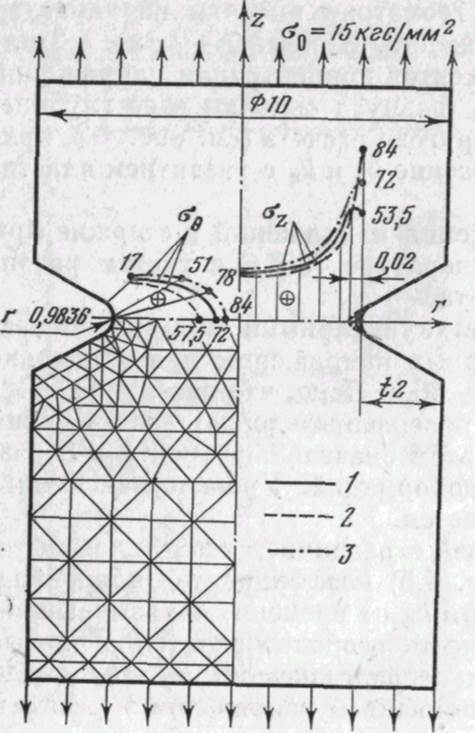
Рис.4.4. Напряженное состояние в стержне с выточкой (t = 22 им, г = 0,9836 мм) при растяжении уси­лиями cf_e = 15 кгс/мм⁸

1 — упругость; 2— пластичность; а — ползучесть

             

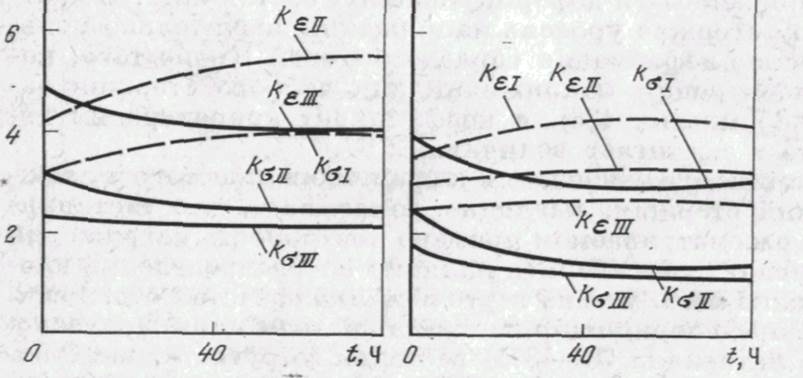
Рис. 4.5. Изменение коэффициентов k_g я k_eво времени

о — а = 60°, ( = 0,915 мм; б — а = 60^е,   1 = 2 мм

         

Рис. 4.6. Распределение напряжений в стержне с выточкой при сложном нагружении через 80 ч (сплошные кривые). Пунктиром показаны напряжения при простом однократном нагружении.

Рис. 4.7. Распределение напряжений в галтели цилиндрического стержня при упругих деформациях, сплошными — при упруго-пластиче­ских деформациях в моменты £ = 0 ч и f = 80 ч. Зона нелиней­ных деформаций заштрихована.

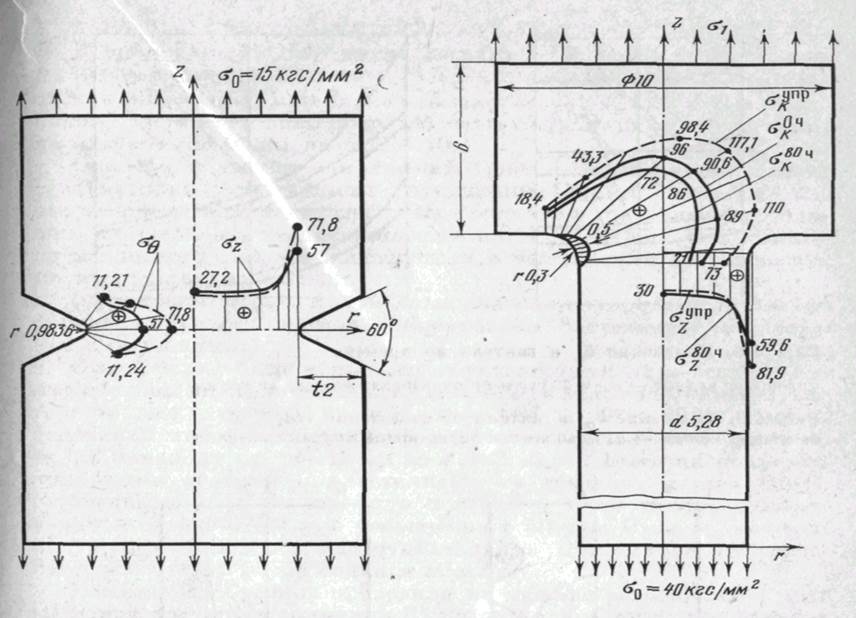
Выполнены и расчеты стержней с радиусами галтелей г = = 0,57 мм и г = 1,2 мм при тех же нагрузках в условиях упру­гости, пластичности, ползучести. Замечено, что по мере увеличе­ния радиуса галтели максимум нормальных напряжений смеща­ется в сторону гладкой части стержня меньшего диаметра, наи­большие напряжения заметно уменьшаются.

На рис. 4.8 и 4.9 приведены кривые, иллюстрирующие умень­шение теоретического коэффициента концентрации с развитием деформаций ползучести (рис. 4.8) и с увеличением радиуса галте­ли (рис. 4.9). Этот типичный пример осесимметричной задачи концентрации напряжений выявляет те же основные закономерности распреде­ления напряжений, что и в стержнях с выточкой (надрезом).

113

       

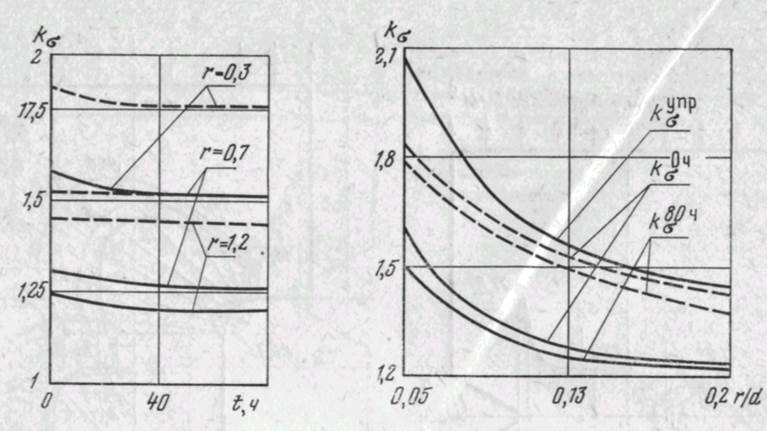
Рис. 4.8. Изменение k_aв галтели во времени Сплошные кривые — а, = 30 кгс/мм¹; пунктирные"— ао = 40 кгс/мм³

Рис. 4.9. Изменение k_gв галтели от отношения ridСплошные кривые — а« = 40 кгс/мм¹; пунктирные — с. = 30 кгс/ым' 0,2 r/d

                   

Рис.   4.10. Результаты   расшифровки  экспериментальных  данных

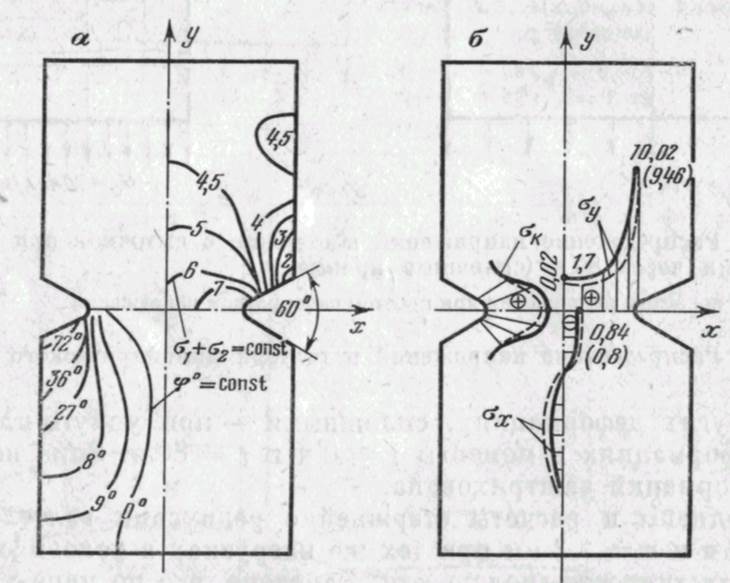
« — изоклины   ф° = const,   изопахики   (ст₍ + 0i= const);   о — эпюры напряжений

Результаты расчета при упругих деформациях сравнивались с данными эксперимента, выполненного поляризационно-оптическим методом. Из оптически активного материала ЭД-6 МТГФА изготавливалась плоская модель конструкции. Такое упрощение связано со значительными техническими трудностями решения объемных задач методом фотоупругости и с большими, трудно оцениваемыми погрешностями подобных экспериментов.

114

Методика исследования соответствовала приведенным в гла­ве 2 примерам. Модель имела ширину b = 50 мм, глубину t= = 10 мм, радиус впадины г = 4,5 мм и угол раствора 60°. Опти­ческая постоянная материала оказалась равной oi⁰ = 35 кгс/см² полос. Результаты испытаний и эпюры напряжений (с пересчетом на натуру) показаны на рис. 4.10.

Опытные значения напряжений (рис. 4.10, сплошные линии) сравнивались с расчетными (пунктирные линии). Установлено, что их значения близки. Небольшое отличие в значениях наиболь­ших напряжений, не превышающее 6,8%, связано с использова­нием плоского аналога конструкции и небольшими погрешностя­ми изготовления моделей.

Сопоставим теперь полученные значения теоретических и эф­фективных коэффициентов концентрации напряжений в стерж­нях с выточками.

С этой целью были испытаны на усталость гладкие и надрезан­ные образцы из стали ЭИ 961(1Х12Н2МФ) с механическими харак­теристиками: а_в = 93 кгс/мм², б = 11,5%, Ч*¹ = 60%. Радиус оснований выточек постоянной глубины с углом раствора а = = 60° изменяли от г = 15 мм до г = 0,45 мм. Выточки получали токарными резцами с пластинками из твердого сплава ВК-8, заточенными с углом профиля а = 60° ± 10 на профилешлифо-вальном станке 395М при увеличении в 50 раз. Размеры выточек контролировались на инструментальном микроскопе. Образцы изготавливались одной садки и плавки.

Испытания образцов проводили на машине резонансного типа [106] при частоте нагружения 63 Гц по методу непосредственного нагружения [106] на базе 10' циклов. Кривые усталости строи­лись по результатам испытаний 10—15 образцов.

Экспериментальные данные сведены в табл. 4.1, где приведе­ны расчетные значения теоретических коэффициентов концентра­ции, полученные расчетным путем.

Анализ показывает, что значения теоретических и эффектив­ных коэффициентов концентрации напряжений находятся в ста­ционарном отношении, что свидетельствует о достоверности рас­четов.

                                                                                                                   Таблица 4.1

                                       Результаты испытаний образцов с надрезом

Материал образца	Тип образца	Радиус скругле-нин г, мм	Предел выносливости ааn(кгс мм2) при тем­пературе испытаний (°С)		Отношение Лгэ/Лга при температуре (°С)
			20°  |   500°		20°      |     500°
ЭИ 961 (1Х12Н2МФ)	С над­резом	0,15 0,30 0,45	10 11 13	5,5 6,0 7,0	2,3 /3,90 2,1 /2,85 1,77/2,37	2,91/3,50 2,67/2,38 2,29/2,04
	Гладкий	—	23	16	—	—

115