


Лабораторная работа "Активные фильтры"
по дисциплине "Основы автоматизации проектирования"
Активными называются фильтры, в состав которых входят цепи с электронными приборами, в том числе операционные усилители (ОУ), а требуемая амплитудно-частотная характеристика формируется за счет цепи отрицательной обратной связи. При замыкании на землю неинвертируемого входа и включении в цепь отрицательной обратной связи по инвертируемому входу сопротивлений согласно схеме рис.1,а ОУ является активным фильтром 1-го порядка, а при схеме рис.2,б - активным фильтром 2-го порядка. Комбинируя включение различных элементов в цепи обратной связи ОУ, можно формировать разнообразные амплитудно-частотные характеристики активного фильтра.
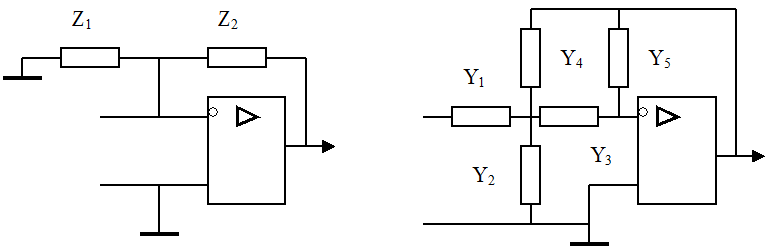
а) Рис.1 б)
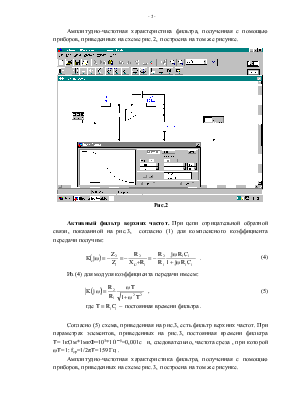
Активный фильтр нижних частот. Комплексный коэффициент активного фильтра 1-го порядка (рис.1,а) определяется выражением:
![]() (1)
(1)
При цепи отрицательной обратной связи, показанной на рис.2, согласно (1) для комплексного коэффициента передачи получим:
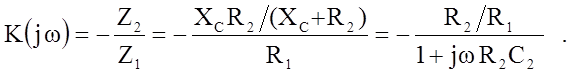
(2)
Из (2) для модуля коэффициента передачи имеем:

(3)
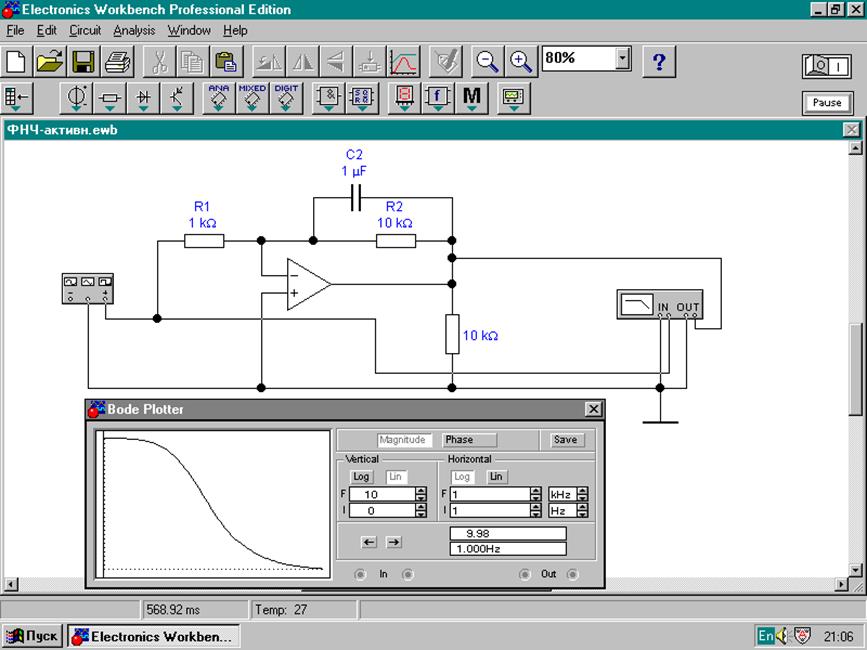
Согласно (3) схема, приведенная на рис.2, есть фильтр нижних частот. При параметрах элементов, приведенных на рис.2, постоянная времени фильтра Т= 10кОм*1мкФ=104*10 ─6=0,01с и, следовательно, частота среза , при которой ωТ=1: fср=1/2πT=15,9 Гц .
Амплитудно-частотная характеристика фильтра, полученная с помощью приборов, приведенных на схеме рис.2, построена на том же рисунке.
 |
Активный фильтр верхних частот. При цепи отрицательной обратной связи, показанной на рис.3, согласно (1) для комплексного коэффициента передачи получим:
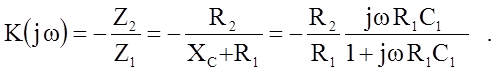
(4)
Из (4) для модуля коэффициента передачи имеем:
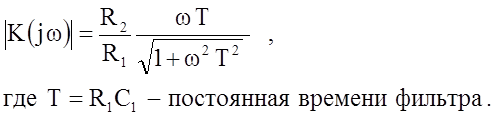
(5)
Согласно (5) схема, приведенная на рис.3, есть фильтр верхних частот. При параметрах элементов, приведенных на рис.3, постоянная времени фильтра Т= 1кОм*1мкФ=103*10 ─6=0,001с и, следовательно, частота среза , при которой ωТ=1: fср=1/2πT=159 Гц .
Амплитудно-частотная характеристика фильтра, полученная с помощью приборов, приведенных на схеме рис.3, построена на том же рисунке.
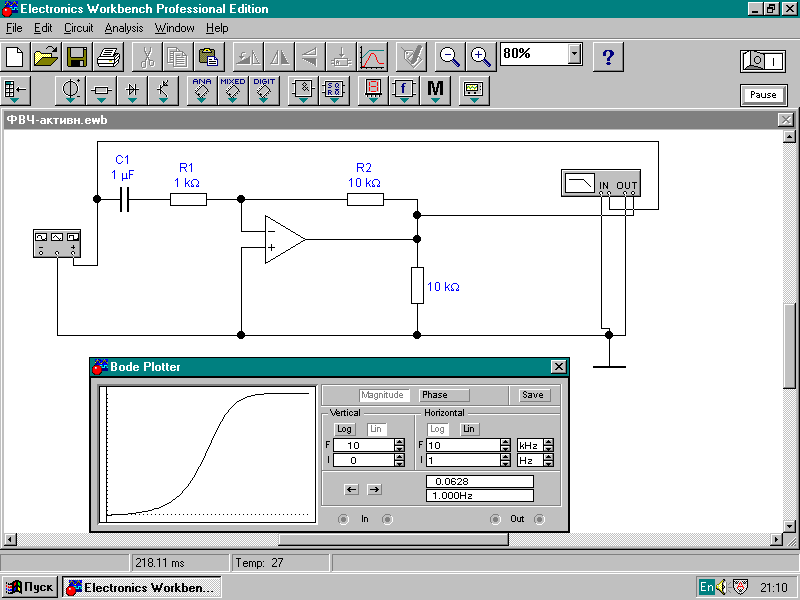 |
Рис.3
Полосовой фильтр активного типа. Комплексный коэффициент активного фильтра 2-го порядка (рис.1,б) определяется выражением:
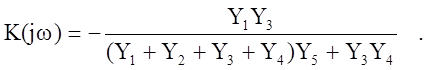
(6)
При данных величинах для модуля комплексного коэффициента передачи из (6) получим:
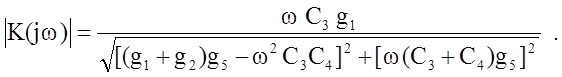
(7)
Согласно (7) схема, приведенная на рис.4, есть полосовой фильтр.
Частота, при которой знаменатель выражения (7) принимает минимальное значение, соответствует центральной частоте полосового фильтра активного типа.
Амплитудно-частотная характеристика полосового фильтра, полученная с помощью приборов, приведенных на схеме рис.4, построена на том же рисунке. При параметрах элементов, приведенных на рис.4, центральная частота полосового фильтра равна 16,79 кГц.
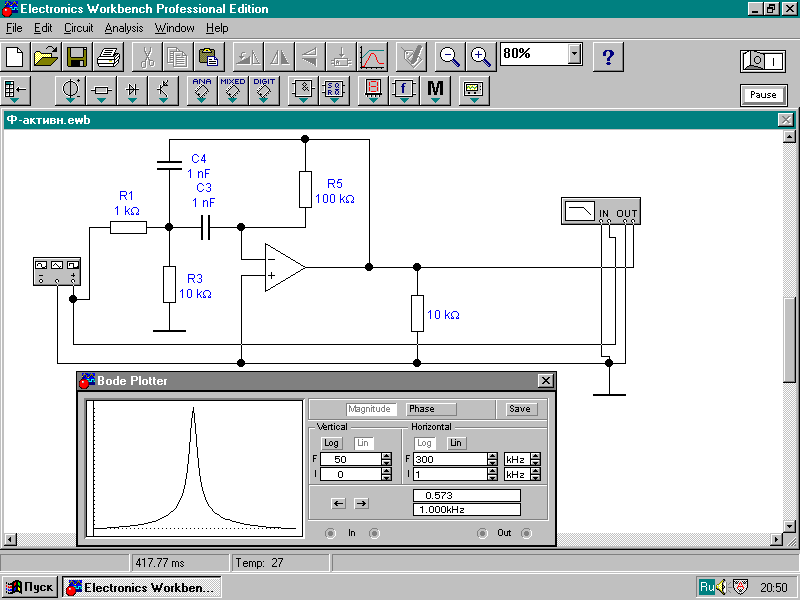 |
Рис.4
Задание на выполнение лабораторной работы.
1. Определите параметры активного фильтра нижних частот (рис.2) с частотой среза в 1кГц. Постройте по аналогии с рис.2 амплитудно-частотную характеристику фильтра.
2. Определите параметры активного фильтра верхних частот (рис.3) с частотой среза в 10кГц. Постройте по аналогии с рис.3 амплитудно-частотную характеристику фильтра.
3. Подберите параметры элементов полосового фильтра активного типа (рис.4) с центральной частотой, близкой 100 кГц.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.