Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ЭЛЕКТРОМЕХАНИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра электромеханики
«ИССЛЕДОВАНИЕ ПРЯМОГО ПУСКА ДВИГАТЕЛЯ НЕЗАВИСИМОГО ВОЗБУЖДЕНИЯ НА ЭВМ»
(Отчёт по лабораторной работе №1)
Выполнил:
![]()
![]()
![]() Студент
гр. ЭМ – 51 «22» сентября 2008 г. Солнцев А.
Студент
гр. ЭМ – 51 «22» сентября 2008 г. Солнцев А.
Проверил:
![]()
![]()
![]() К.т.н.,
доцент « » 2008
г. Пастухов В.В.
К.т.н.,
доцент « » 2008
г. Пастухов В.В.
Новосибирск 2008
Краткое теоретическое введение:
Прямым (безреостатным) пуском двигателя постоянного тока с независимым возбуждением будем называть такой пуск, при котором токи в обмотках возбуждения и якоря создаются независимыми источниками, и якорная обмотка непосредственно подключена к сети на её полное напряжение.
Исследование такой электрической машины очень важно с точки зрения определения её быстродействия, т.е. оценки времени переходного процесса от пуска двигателя до выхода его на номинальный режим работы, зависящего от ряда параметров.
Переходной процесс, происходящий в ДПТ НВ при прямом пуске, мы будем исследовать на основе его математической модели, которая представляется виде системы двух уравнений:
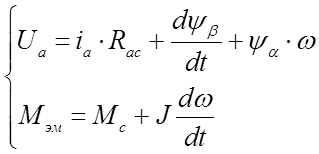
В данной системе:
![]() ,
, ![]() − напряжение и ток цепи якоря;
− напряжение и ток цепи якоря;
![]() − собственное
потокосцепление обмотки якоря по оси β;
− собственное
потокосцепление обмотки якоря по оси β;
![]() − потокосцепление
обмотки возбуждения с обмоткой якоря по оси α;
− потокосцепление
обмотки возбуждения с обмоткой якоря по оси α;
![]() − эдс, наводимая в
якоре в результате его вращения в поле обмотки возбуждения (противо эдс);
− эдс, наводимая в
якоре в результате его вращения в поле обмотки возбуждения (противо эдс);
![]() − электромагнитный
момент.
− электромагнитный
момент.
Данная система получена при следующих допущениях:
1. К моменту подключения цепи якоря, ток возбуждения и основной магнитный поток создаваемый обмоткой возбуждения должны быть установившимися, для создания наибольшего момента;
2.
Ток
возбуждения много меньше тока якоря (т.к. сопротивление якоря мало и в
начальный момент времени противо эдс равна нулю) поэтому считаем, что ![]() ;
;
3. щетки установлены на геометрической нейтрали, поперечная и коммутационная реакции якоря отсутствуют в течение всего переходного процесса, величина магнитного потока остается неизменной;
4. индуктивность
![]() и сопротивление якорной цепи
постоянны.
и сопротивление якорной цепи
постоянны.
Решение этой системы можно осуществить, опираясь на операционное исчисление. В соответствии с этим все интегро-дифференциальные соотношения переводятся в изображения и представляются в виде алгебраических, что существенно облегчает расчёт.
Найдя изображение искомой величины можно найти её оригинал при помощи обратного преобразования.
Процесс пуска ДПТ НВ можно разбить на два этапа:
· на
первом этапе двигатель неподвижен, значит, в системе остаётся только первое
уравнение, без учёта последнего слагаемого. После решения этого уравнения
операторным методом мы получим выражение для тока якоря 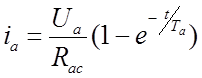 .
.
Т.к. ток якоря возрастает, то вместе с ним увеличивается и электромагнитный момент. Время, при котором электромагнитный момент станет равным моменту нагрузки, называется временем трогания, которое запишется так:
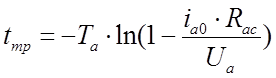 .
.
· На втором этапе рассматриваются оба уравнения математической модели, основной частью решения, которых является поиск корней, по виду которых можно будет судить о режиме переходного процесса.
Различают три режима переходных процессов: апериодический (корни действительные отрицательные), колебательный (корни комплексные с отрицательной действительной частью) и режим, при котором система находится на границе между этими двумя режимами.
В общем виде корни имеют вид:
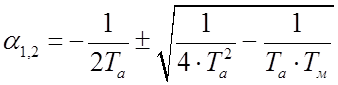 .
.
Из выражения следует, что при значении
постоянной времени ![]() корни
действительные (процесс апериодический), а при
корни
действительные (процесс апериодический), а при ![]() −
комплексные (процесс колебательный затухающий).
−
комплексные (процесс колебательный затухающий).
О решении дифференциальных уравнений операторным методом:
Суть метода заключается в замене производной оператором «р»:
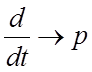 .
.
![]()
После замены из получившегося алгебраического
уравнения выражается искомая функция, которая представляется в виде правильного
отношения полиномов 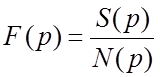 . Приравняв,
. Приравняв, ![]() находим его корни.
находим его корни.
Пользуясь теоремой разложения, переходим к оригиналу:
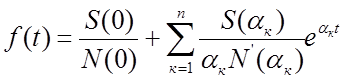 .
.
Если начальные условия не нулевые, то переход к изображению осуществляется по следующей формуле:
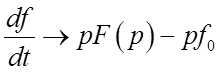 .
.
Цель работы:
Исследовать пуск двигателя постоянного тока независимого возбуждения.
Получить практические навыки моделирования прямого пуска двигателя постоянного тока независимого возбуждения на ЭВМ.
Задание на работу:
1. Определить влияние постоянных времени на пуск двигателя;
2. Выполнить анализ влияния электромагнитной постоянной цепи якоря на процесс задаваясь последовательно несколькими значениями постоянной цепи якоря.
Электромагнитную постоянную изменять за счет изменения индуктивности якоря, следя, за тем, чтобы активное сопротивление обмотки якоря оставалось постоянным;
3. Выполнить анализ влияния электромеханической постоянной изменяя момент инерции относительно заданного при постоянной величине электромагнитной;
4. Снять и проанализировать характеристики. Сделать выводы.
Вариант ДПТ №9
Исходные данные:
Мощность, кВт: 1.6;
Частота вращения, об/мин: 750;
КПД, %: 68.5;
Активные сопротивления обмоток при 15°С, Ом:
Обмотки якоря: 1.88;
Дополнительных полюсов: 1.39;
Возбуждения: 35;
Напряжение обмотки якоря, В: 220;
Индуктивность обмотки якоря, мГн: 38.6;
Момент инерции, кГ*м2: 0.038.
Расчёт по исходным данным:
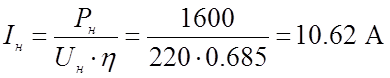 − номинальный ток якоря;
− номинальный ток якоря;
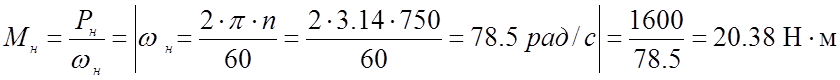 − номинальный момент;
− номинальный момент;
![]() − суммарное активное сопротивление якорной цепи при
температуре 150С;
− суммарное активное сопротивление якорной цепи при
температуре 150С;
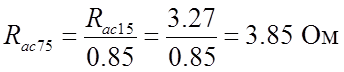 − суммарное активное сопротивление
якорной цепи при температуре 750С,
− суммарное активное сопротивление
якорной цепи при температуре 750С,
где k=0.85 – коэффициент теплового сопротивления;
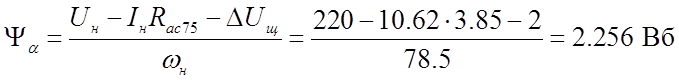 − потокосцепление обмотки якоря по оси α, где
− потокосцепление обмотки якоря по оси α, где ![]() − падение напряжения на щётках;
− падение напряжения на щётках;
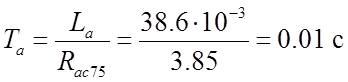 − электромагнитная постоянная обмотки якоря;
− электромагнитная постоянная обмотки якоря;
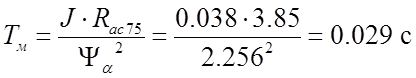 − электромеханическая постоянная.
− электромеханическая постоянная.
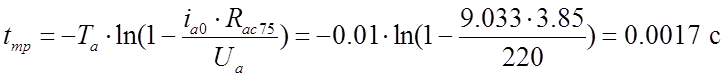 − время трогания,
− время трогания,
где 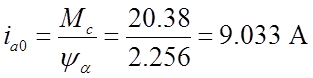 − ток, при котором начинается
трогание якоря.
− ток, при котором начинается
трогание якоря.
Экспериментальная часть:
1. Изучение влияния электромагнитной постоянной времени:
Данные опыта занесём в таблицу 1.
Таблица 1. Данные опыта №1
|
|
0.01 |
0.007 |
0.02 |
|
|
2.861 |
4.12 |
1.43 |
|
|
0.0017 |
0.0011 |
0.0034 |
|
Цвет графика |
красный |
зелёный |
голубой |
На рисунке 1 представлены экспериментальные зависимости.
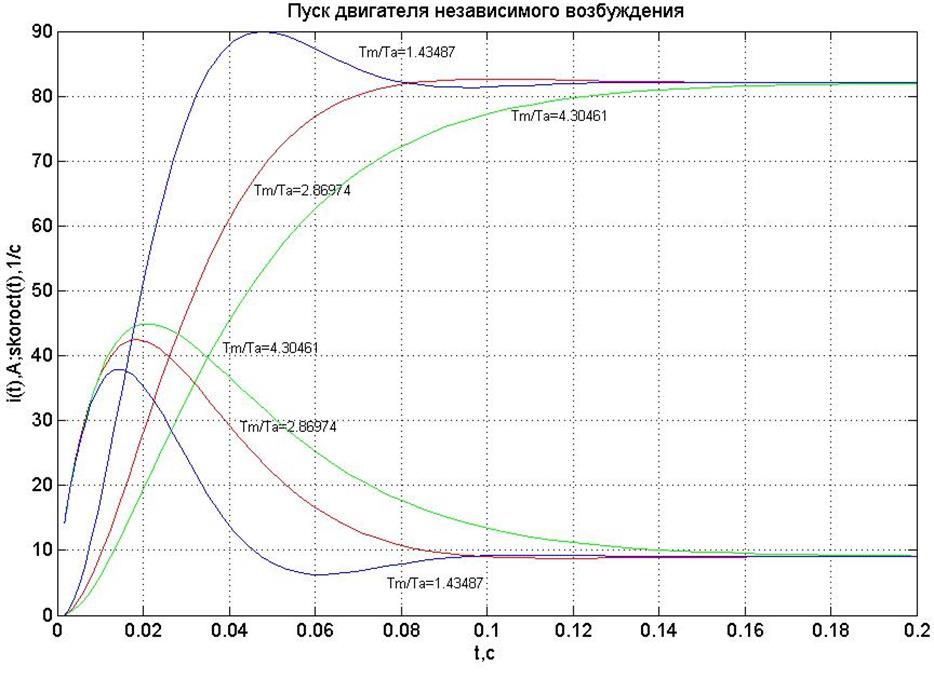
Рисунок 1 Экспериментальные зависимости
2. Изучение влияния электромеханической постоянной времени:
Данные опыта занесём в таблицу 2.
Таблица 2. Данные опыта №2
|
|
0.038 |
0.057 |
0.019 |
|
|
2.861 |
4.29 |
1.43 |
|
|
0.0017 |
0.0017 |
0.0017 |
|
Цвет графика |
красный |
зелёный |
голубой |
На рисунке 2 представлены экспериментальные зависимости.
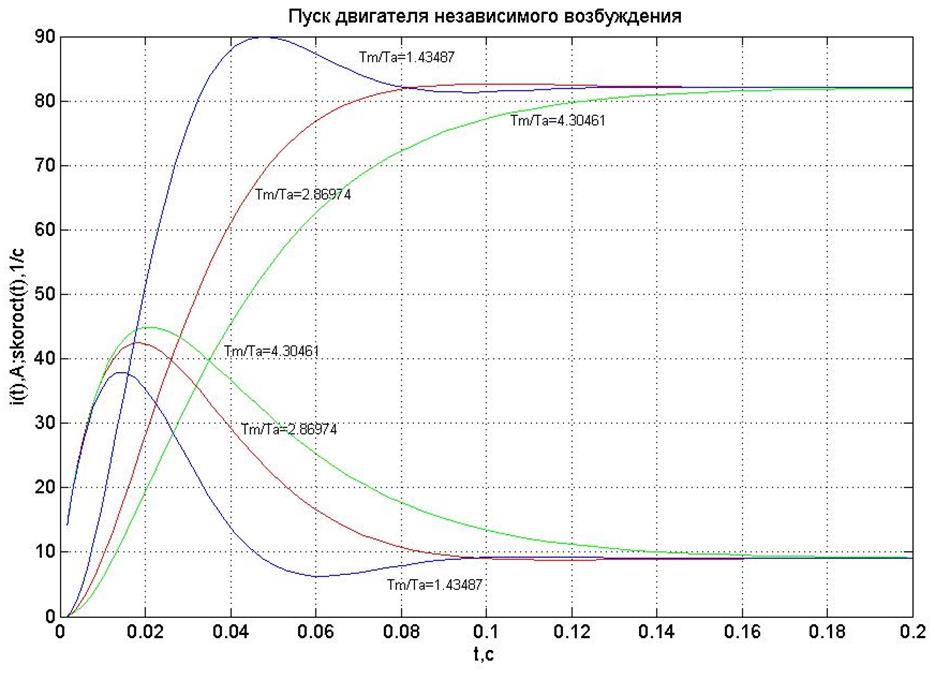
Рисунок 2 Экспериментальные зависимости
Выводы по лабораторной работе:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.