Проектирование и техническая эксплуатация систем документальной электросвязи: Методические рекомендации по выполнению курсового проекта, страница 5

На первом этапе проведения расчетов необходимо выполнить численный статистический анализ входящего потока СМО.   Анализ  величины входящего потока производится на основании  рисунка  исходных данных курсового проекта.

Наиболее важным параметром для определения нагрузки на систему является характер поступления заявок.  Поскольку события, приводящие к занятию одного из каналов системы, поступают в случайные моменты времени, то число заявок, поступающих  в заданный интервал времени, представляет собой простейший поток и может быть описано предельным случаем биноминального распределения, известного как распределение Пуассона:

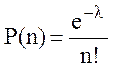  ,                                                                                                                               (29)

где  P(n)  -  вероятность поступления n заявок в заданный интервал времени;

l -  среднее значение n для заданного временного интервала;

n -  количество заявок, поступивших в заданный временной интервал.

Для анализа закономерностей, которым подчинены массовые случайные явления, целесообразно использовать аппарат математической статистики.

Пусть из генеральной совокупности извлечена выборка, причем x₁ наблюдалось n₁ раз, x₂ – n₂ раз, x_k – k раз. И  n - объем выборки. Наблюдаемые значения называются вариантами, а последовательность вариант, записанных в возрастающем порядке - вариационным рядом. Числа наблюдений называют частотами.

Статистическим распределением выборки называют перечень вариант и соответствующие им частоты. Статистическое распределение  можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).

В целях наглядности строят различные графики статистического распределения. В случае непрерывного признака целесообразно стоить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбиваются на несколько частичных интервалов длиною h и находят для каждого частичного интервала  n_i сумму частот вариант, попавших в i интервал.

Гистограммой называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению (плотность частоты). Площадь i -того частичного прямоугольника равна сумме частот вариант i интервала, следовательно, площадь гистограммы равна сумме всех частот, т.е. объему выборки.

Для выяснения закономерности распределения числа заявок по длительности пребывания в системе необходимо по рисунку составить вариационный ряд и по вариационному ряду оценить статистическое распределение выборки. Необходимо составить таблицу следующего вида:

Частичный интервал длиною h	Общий объем выборки N =
	Сумма частот вариант частичного интервала ni	Плотность частоты

На основании анализа указанной таблицы производится расчет интенсивности входящего потока:

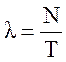,                                                                                                                                (30)

где      N - количество заявок, поступивших на вход системы, штук.

            T - рассматриваемый интервал времени, сек (рассматриваемый период - 30 дней).

Математическое ожидание длительности обслуживания (среднего времени работы пользователя с узлом сети):

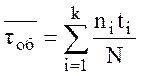.                                                                                                                    (31)

Интенсивность потока обслуживания:

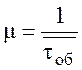 .                                                                                                                             (32)

Задача синтеза оптимальной структуры СМО решается на основе анализа возможных вариантов при заданных параметрах. Поскольку для СМО с отказами вероятность занятости всех каналов является одновременно и вероятностью отказа, необходимо обеспечить такое значение нагрузки системы, при котором она бы справлялась с обслуживанием большинства заявок.  Для определения оптимального количества модемов (приборов для обслуживания) необходимо провести сравнительный анализ состояний системы в зависимости от количества каналов обслуживания m.