Проектирование и техническая эксплуатация систем документальной электросвязи: Методические рекомендации по выполнению курсового проекта, страница 4

Следующий этап расчетов заключается в определении оптимального распределения канальных емкостей C_i, . Расчет канальных емкостей выполняется для ряда коэффициентов загрузки r. Рассчитанные величины l_i могут служить основой для предварительной оценки величины каждой канальной емкости. Если в качестве канальной емкости взять величину, пропорциональную l_i, то коэффициент загрузки каналов в этом случае будет составлять 100%. При изменении маршрута следования сообщений такая сеть может оказаться неработоспособной, так как величины l_i «жестко привязаны» к определенному пути следования сообщений. Для того чтобы сеть была работоспособной необходимо обеспечить минимальную загрузку каждого канала. Уровень загрузки определяется коэффициентом загрузки r. Перед проведением расчетов оптимального распределения канальной емкости для каждого канала, необходимо предварительно рассчитать величину общей распределяемой канальной емкости. Расчет производится на основании следующих формул:

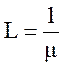,                                                                                                                                               (19)

где m - интенсивность потока обслуживания, 1/бит.

Тогда общая емкость сети вычисляется по формуле:

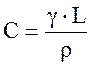.                                                                                                                           (20)

Рассчитаем значение общей емкости сети при r = 0,1:

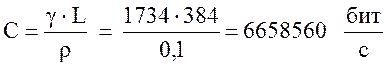 .                                                                         (21)

Полученная общая емкость  С  далее будет распределяться по v каналам, согласно следующему соотношению:

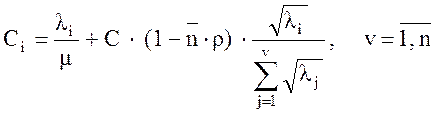   .                                                               (22)

Приведем пример распределения нагрузки канала при r = 0,1:

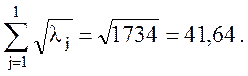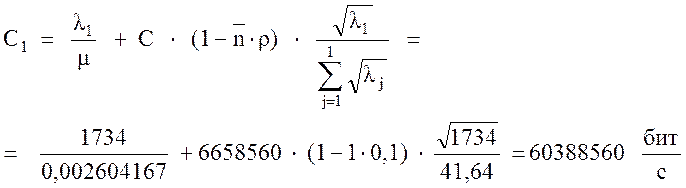     (23)              

                         (23)  

Далее выполняются расчеты времени задержки сообщений по формуле:

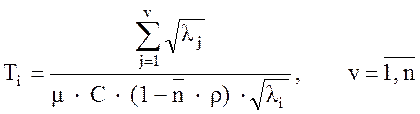                                                                                 (24)

Рассчитаем  время задержки передачи сообщений для канала при r = 0,1:

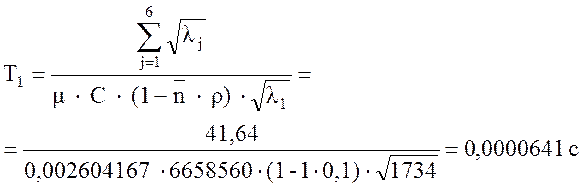                                          (25)

Таким образом, рассчитываются значения С_i и T_i для всех каналов сети. Кроме того, рассчитываются  параметры С, С_i и T_i при других значений коэффициента загрузки r (0,2 – 0,9), полученные значения представлены в таблице 7.

При появлении отрицательных значений можно говорить о перегрузке в сети.  Расчет производится при условии  < 1.

Общая  задержка сети рассчитывается по формуле:

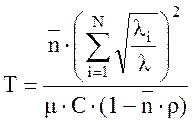.                                                                                                                      (26)

Рассчитаем значение задержки при r = 0,1:

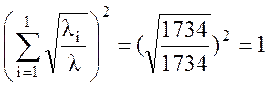  .                                                                                            (27)

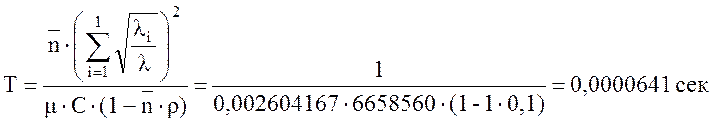                (28)

Для остальных значений коэффициента загрузки рассчитанные значения задержки в сети представлены в таблице 8.

Далее с использованием рассчитанных значений величины задержки в каждом канале производится построение графика функциональной зависимости T = f (r), где T - общее время задержки в сети, рассчитанное при использовании соотношения (26).  В качестве аргумента для построения функции берется ряд значений r согласно заданию на курсовое проектирование. После проведения построения необходимо сделать выводы. Если  исходные значения r не дают полного представления о поведении функции T = f (r) необходимо дополнить исходные данные (аргумент) функции рядом значений r с другим шагом и провести повторный пересчет функциональной зависимости.

Методика выполнения 2 задания.

Предполагается, что исходными данными для проведения расчетов являются экспериментально полученные статистические сведения о характере загрузки узла удаленного доступа. Физически узел удаленного доступа состоит из m модемов, которые подключены к автоматической телефонной станции. Пользователи в случайные моменты времени осуществляют звонки на узел. Если пользователь получил обслуживание (АТС не перегружена, есть свободные соединительные линии и т.д.), то он занимает на определенный промежуток времени  прибор для обслуживания. Если в какой-либо из моментов времени  очередной пользователь, осуществив звонок на узел, застает все модемы (приборы для обслуживания) занятыми, то он получает отказ в обслуживании. Таким образом, описываемая система с точки зрения теории СМО представляет собой систему с отказами. В каждый момент времени в системе может находиться не более m заявок.