Основные уравнения электродинамики в дифференциальной форме

2 ОСНОВНЫЕ УРАВНЕНИЯ ЭЛЕКТРОДИНАМИКИ В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ

До сих пор рассматривались уравнения электродинамики в интегральной форме, справедливые для всего объема, учитывали лишь суммарный эффект большого количества зарядов. При использовании ЭМП важно знать ЭМП в каждой точке объема, то есть нужно знать уравнения в дифференциальной форме записи.

Уравнения Максвелла. Первое уравнение Максвелла является обобщением закона полного тока (1.23), запишем его через плотности токов:

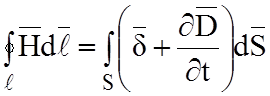
К дифференциальной форме можно перейти путем предельного перехода, а именно, контур интегрирования ℓ сжимается в точку, при этом поверхность, стягиваемая контур, также стремится к нулю. В итоге в правой части останется подинтегральное выражение 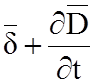 , а в левой части будет циркуляция вектора  через бесконечно малый контур, который обозначается rot:

rot= 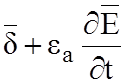                                                                (2.1)

Можно также использовать теорему Стокса 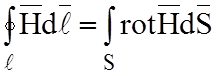.  rot есть пространственная производная, определяет зависимость вектора  от пространственных координат, это вектор и берется от вектора. Если rot¹0 ,это есть признак вихревого ЭМП, то есть согласно (2.1) силовые линии вектора  всегда замкнуты сами на себя, магнитное поле всегда вихревое. Источником магнитного поля являются электрические токи проводимости и переноса и изменяющееся во времени электрическое поле. Вектор  и вектор rot взаимно перпендикулярны.

Рассмотрим ориентацию векторов в уравнении (2.1). Это векторное уравнение, из равенства векторов следует их ориентация (рисунок 1.5). Силовые линии вектора  - замкнутые концентрические окружности, охватывающие векторы плотности токов 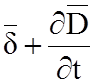 проводимости и смещения находящиеся в плоскости перпендикулярной векторам rot и 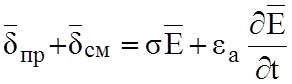. Отсюда следует, что векторы  и  взаимно перпендикулярны (). Направление вектора  и векторов плотностей токов проводимости и смещения 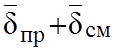 составляют правовинтовую систему. Если источники (t) и 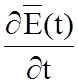 есть функции времени, то они будут создавать вихревое и переменное магнитное поле  (t), если нет, то они создают вихревое и независящее от времени магнитное поле.

Второе уравнение Максвелла есть обобщение закона электромагнитной индукции Фарадея (1.15). Применяя тот же предельный переход, получим второе уравнение Максвелла в дифференциальной форме:

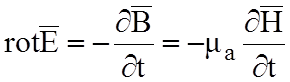                                                     (2.2)

Из него следует, что источником вихревого и переменного электрического поля является переменное  магнитное поле. Знак минус указывает на противоположное направление векторов rot  и 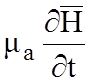 , векторы rot и  перпендикулярны друг другу и составляют правовинтовую систему (рисунок  1.5). Векторы rot и rot замкнуты сами на себя и перпендикулярны друг другу.

Третье и четвертое уравнения Максвелла являются обобщением закона Гаусса для электрического и магнитного полей. Дифференциальная форма этих уравнений получается путем предельного перехода при устремлении  объема к нулю. При этом правая часть для электрического поля будет равна объемной плотности заряда 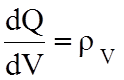, а левая есть поток вектора  через бесконечно малую поверхность dS объема dV. Этот поток называют дивергенцией. В результате получаются уравнения в дифференциальной форме для электрического и магнитного полей

div=ρ_V,  div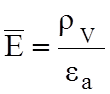                                              (2.3)

div=0,  div=0                                                     (2.4)

Дивергенция определяет наличие или отсутствие источников поля векторов  и  в конкретной точке. Если дивергенция равна нулю (2.4), это говорит о том, что отсутствуют источники магнитного поля, в виде магнитных зарядов. Нет таких точек в любом объеме, где div≠ 0, div≠ 0, то есть в природе нет магнитных зарядов. Для электрического поля (2.3) такие точки есть, в них находятся электрические заряды с объемной плотностью ρ_V, конечно есть точки, в которых отсутствуют электрические заряды, тогда в них div=0, div0. Нужен расчет, нахождение дивергенции как функции координат точек объема. Причем если div0, в данной точке находится источник электрического вектора, а именно положительный заряд, силовые линии вектора   начинаются на положительном заряде, если div<0, в точке находится отрицательный заряд и силовые линии здесь заканчиваются, это «сток». Если div=0, в точке нет зарядов (нет «стоков» и «истоков») и силовая линия проходит эту точку, не прерываясь, что и происходит для магнитного поля.

Закон сохранения заряда. Уравнение непрерывности полного тока. Эти уравнения являются следствием уравнений Максвелла.

Получим дивергенцию первого уравнения Максвелла

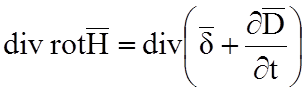=0,

так как =0, используя третье уравнение Максвелла div=ρ_V, получим из правой части:

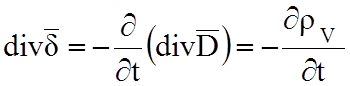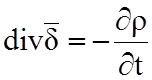;                      (2.5)

Если из данной точки истекают положительные заряды, то ∂ρ<0, а >0 и в точке находится «исток», здесь начинаются силовые линии вектора . Сумма

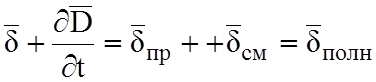
Тогда =0 и вектор плотности полного тока в любой точке непрерывен.

Полная система уравнений Максвелла.

Уравнения (2.1, 2.2, 2.3, 2.4) являются основными, при решении конкретных задач их недостаточно, необходимо учитывать особенности среды. Основные уравнения дополняют материальными уравнениями, которые характеризуют влияние среды на протекающие в ней электромагнитные процессы.

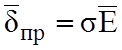; ; ,                                       (2.6)

где ε_а, μ_а, σ – макроскопические параметры среды, в каждой точке постоянны и считаются известными.

Если рассматривать объем, где имеются первичные источники поля , , то основные уравнения запишутся так:

1)

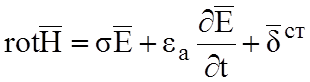
2)

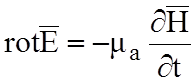
3)

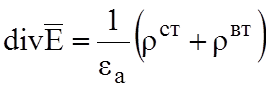
4) ,                                                                                                   (2.7)

где  – объемная плотность вторичных зарядов.

Первичные и вторичные заряды подчиняются аналогичному закону (2.5). Из первого уравнения (2.7) следует:

; ;

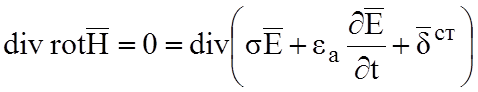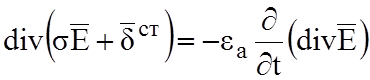заменив  из третьего уравнения (2.7), получим

;

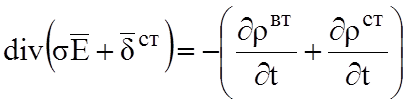откуда

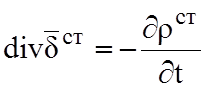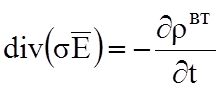;                                 (2.8)

Релаксация зарядов.