Условия единственности решений уравнений электродинамики

4 УСЛОВИЯ ЕДИНСТВЕННОСТИ РЕШЕНИЙ УРАВНЕНИЙ    

   ЭЛЕКТРОДИНАМИКИ

             Уравнения Максвелла являются дифференциальными уравнениями в частных производных, поэтому допускают множество решений. Из общих физических представлений очевидно, что при полном повторении условий эксперимента распределение электромагнитного поля должно быть одинаковым. Следовательно, в каждом конкретном случае ЭМП должно удовлетворять не только уравнениям Максвелла, но и некоторым дополнительным требованиям. Какие должны быть эти требования отвечает теорема единственности. Если решение электрической задачи удовлетворяет условиям единственности, то можно быть уверенными, что именно оно определяет существующее на практике ЭМП.

             Большинство задач электродинамики разделяют на внутренние краевые задачи и внешние. Для внутренней задачи требуется найти решение внутри замкнутого объема V₁ , ограниченного поверхностью S. Во внешней задаче ищется решение вне объема V₁ . Теорема единственности для внутренней задачи утверждает, что внутри объема V₁ ,ограниченного поверхностью S, решение уравнений Максвелла для комплексных амплитуд.

                                        ;  

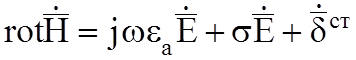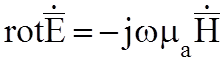
единственно, если во-первых, оно удовлетворяет одному из трех краевых условий:

1.  заданным на поверхности S значением тангенциальной составляющей

вектора ;

2.  заданным на поверхности S значением ;

3.  заданным на части поверхности S значением , и на остальной части S значением ,

-  и если во-вторых, при отсутствии потерь (s=0) частота w не совпадает ни с

одной из резонансных частот области V_1. Если при s=0 частота совпадает с одной из резонансных частот, решение будет неоднозначным.

Единственность решения внешней задачи доказывается при условии, что все сторонние источники распределены на конечном расстоянии от начала координат. Внешняя задача решается для безграничного объема V, ограниченного поверхностью S, исключающей внутренний объем V₁, и бесконечной удаленной поверхности S_¥.(рисунок 2.3).

Условия единственности решения внешней задачи:

1.  на поверхности S таким же условиям, что и при решении внутренней задачи;

2.  в среде без потерь (s=0) при R®¥ условием излучения (4.1);

3.  в среде с потерями (s¹0) условием на бесконечности.

             Условия излучения:

;

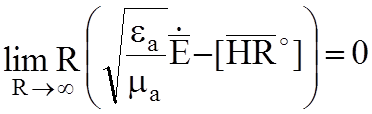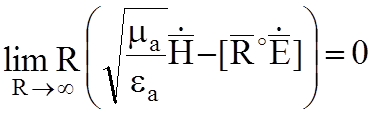
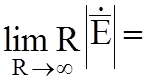        конечной величине; 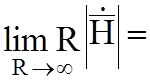конечной величине          (4.1)

             Физически условия излучения означают, что на больших расстояниях от источников, создаваемые ими поля имеют характер сферических бегущих волн, расходящихся от источников в радиальных направлениях.

             Амплитуды векторов поля  и волн убывают на больших расстояниях от источников по закону .

             В безграничной среде с потерями (s¹0) условия излучения заменяют условиями на бесконечности:

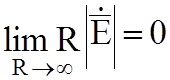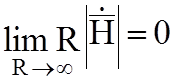                                       ;                                           (4.2)

Они означают, что при наличии потерь векторы поля на больших расстояниях от источников убывают быстрее чем , то есть ,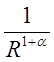

             где a - положительное число.

В реальных условиях удельная проводимость s¹0, поэтому из (4.2) следует, что при R®¥, .